Study and Operation of the DC Speed and Position Control Setup 
Theory
DC Machine
In the dc machine, the field winding is placed on the stator and the armature winding on the rotor. A dc current is passed through the field winding to
produce flux in the machine. Voltage induced in the armature winding is alternating. A mechanical commutator and a brush assembly function as a rectifier or inverter, make the
armature terminal voltage unidirectional.
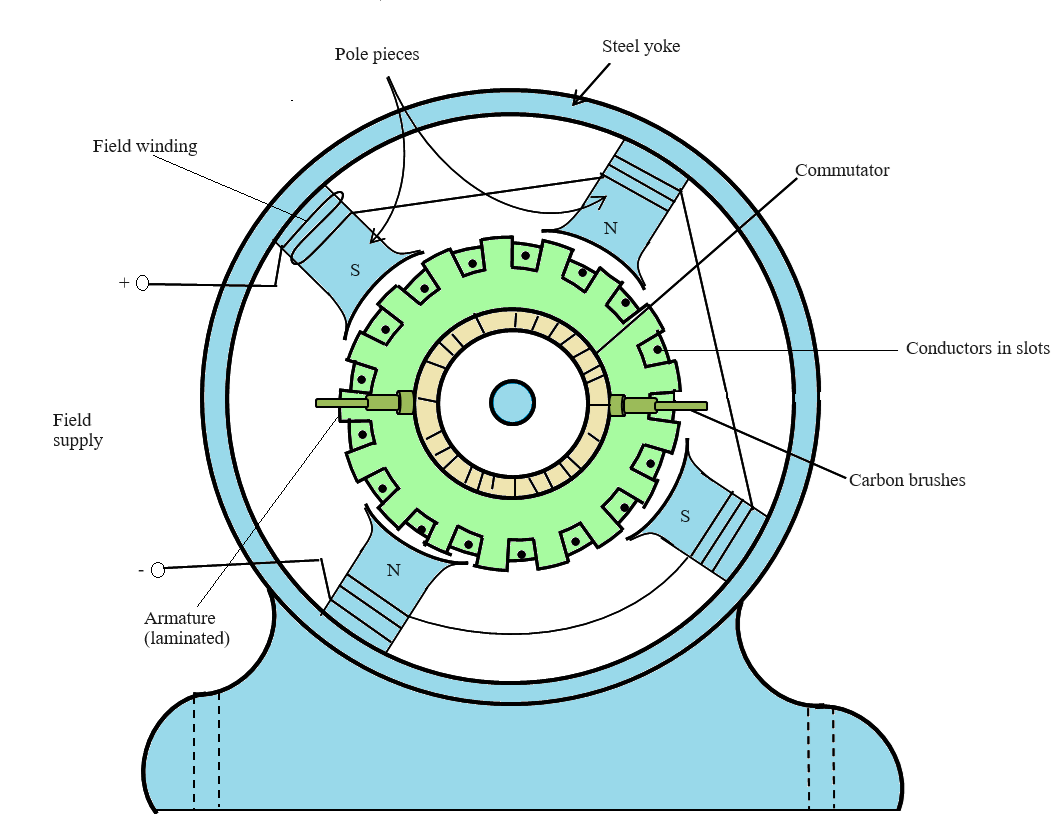
Fig. 1. Cross section view of a dc machine
Application
Although a dc machine can be operated as either a generator or a motor, at present its use as a generator is limited because of the wide spread use of ac power. The dc machine is extensively
used as a motor in industry. Its speed can be controlled over a wide range with relative ease. Large dc motors (in tens or hundreds of horsepower) are used in machine tools, printing
presses, fans, pumps, hoists, cranes, paper mills, textile mills, rolling mills and so forth. Additionally, dc motors still dominate as traction motors used in transit cars and locomotives.
Small dc machines (in fractional horsepower rating) are used primarily as control devices, such as tachogenerators for speed sensing and servomotors for positioning and tracking.
The dc machine definitely plays an important role in industry.
Speed Control of DC Motors
The term 'speed control' stands for intentional speed variation, carried out manually or automatically. Natural speed change due to load, is not included in the term 'speed control'.
DC motors are most suitable for wide range speed control and are therefore indispensable for many adjustable speed drives. The speed of a dc motor is given by below equation.
$$\omega = \frac{V_t - I_a r_a}{K_a \Phi} \tag 1$$
where
$$K_a = \frac{PZ}{2\pi A}$$
where
ω = Angular speed of the dc motor
Vt = Terminal voltage of dc motor
Ia = Armature current of dc motor
ra = Armature resistance of dc motor
P = Number of poles of dc motor
Z = Number of armature conductors of dc motor
A = Number of parallel paths of dc motor
Φ is the magnetic flux
There are basically three methods of speed control and these are
(i) Variation of resistance in the armature circuit
(ii) Variation of the field flux
(iii) Variation of the armature terminal voltage
Before describing these methods, it is preferable to define the terms base speed, speed regulation, speed range, constant power drive and constant torque drive.
Base Speed
It is defined as the speed at which a motor runs at rated armature voltage and rated field current. Base speed is equal to the rated speed or nameplate speed of the motor.
Speed regulation
If the speed-change from no load to full load is Δωm then speed regulation is defined as the ratio of
Δωm to rated speed (or base speed) ωm.
Hence the percentage speed regulation (Sr) is,
$$S_r = \frac{\Delta \omega_m}{\omega_m}\times 100 \ \ \tag 2%$$
Speed range
It is defined as the ratio of the maximum allowable speed to minimum allowable speed of the motor. When the speed range of a motor is specified, it must be mentioned
whether this speed range is at no-load, full load or a fraction of full load.
Constant power drive
If the motor shaft power (shaft torque × speed) remains constant over a given speed range, the system is called a constant power drive. In constant
power drive, higher torques are available at lower speeds and lower torques at higher speeds. The motor size is always decided by the highest torque requirement at the lowest speed.
Constant torque drive
If the motor shaft torque remains constant over a given speed range, the system is called a constant torque drive. In constant torque drive, shaft
power varies as the speed varies.
Magnetic Braking
Conventional braking systems in cars and bicycles utilise the friction force between two objects pressed together to slow an object down. By making use of eddy currents,
magnetic braking can be achieved where the electromagnetic force between a magnet and a conductor in motion is used to create a repulsive and slowing force. If a conductor moves
past a stationary magnet, eddy currents will be induced in the conductor by the magnet, according to Faraday’s law of induction. Eddy currents create their own magnetic field that
opposes the original magnetic field of the magnet. This in turn creates a drag force between the magnet and the conductor, which slows the conductor down.
A permanent magnet or an electromagnet can be used to create the magnetic field in a magnetic brake. A big advantage with magnetic braking is the lack of physical contact
between components. A disadvantage with magnetic braking is that when there is no motion between the magnet and conductor,
there is no static force to maintain the conductor at rest. In this case, the magnetic braking system would need to be supplemented by a friction based (conventional) braking system
like a hand brake.
Speed Control
There are numerous applications where control of speed is required, as in rolling mills, cranes, hoists, elevators, machine tools, transit system and locomotive drives.
DC motors are extensively used in many of these applications. Control of the speed of dc motors below and above the base (or rated) speed can easily be achieved.
Besides, the methods of control are simpler and less expensive than those applicable to ac motors. In the classical method, a Ward–Leonard system with rotating machines is used for speed control of dc motors. Recently,
solid-state converters have been used for this purpose. In this section, various methods of speed control of dc motors are discussed.
In order to achieve wider speed control range, speeds below base speed are obtained by voltage control and above base speed by field flux control.
1. Armature voltage control (Va)
In the armature voltage control mode, the speed control is carried out with rated armature current and constant motor field flux. A constant torque upto base speed is obtained.
Power (torque × speed) increases in proportion to speed. Thus constant torque and variable power drive is obtained upto base speed
with armature terminal voltage control method as shown in Fig. 2.
2. Field current control (If)
The field current control mode is used to obtain speed above the base speed. In this mode, the armature voltage Va remains constant and
the motor field current is decreased (field weakening) to obtain higher speeds. The armature current can be kept constant, there by operating the motor in a constant horsepower mode. The torque obviously decreases as speed
increases. Thus constant power and variable torque drive is obtained above base speed
with field current control method as shown in Fig. 2.
3. Armature resistance control method
The armature resistance control is based on the principle that the speed of the motor is directly proportional to the back emf.
So, if the supply voltage and the armature resistance are kept at a constant value, the speed of the motor will be directly proportional to the armature current.
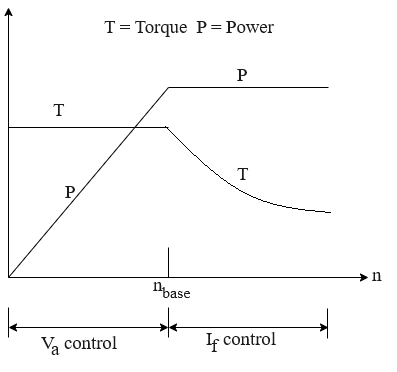
Fig. 2. DC Motor speed control methods graphical analysis
Besides these there are other speed control methods like ward leonard system , Solid-state control using choppers and controlled rectifiers etc.
Open loop speed control
As shown in Fig. 3 , the armature-controlled dc motor is itself a feedback system, where back emf voltage is proportional to the speed of the motor.
The system may be arranged in input-output form such that Va(s) is the input and
ω(s) is the output.
The mathematical expression for open loop speed control is,
$$\omega(s) = \frac{\frac{ k_T}{R_a J}}{\frac{L_a}{R_a}s^2 + (1 + \frac{B L_a}{R_a J} )s + \frac{k_T k_b + R_a B}{R_a J}} V_{a}(s) \tag 3$$
The ratio La/ Ra is called the motor electric-time constant, which makes the system speed response transfer function second order and is denoted by τe. La in the armature circuit is very small, τe is neglected, resulting in the simplified transfer function of the system. Thus, the speed of the motor shaft may be simplified to
$$\omega(s) = \frac{\frac{k_T}{R_a J}}{s + \frac{k_T k_b + R_a B}{R_a J}}V_a(s) \tag 4$$
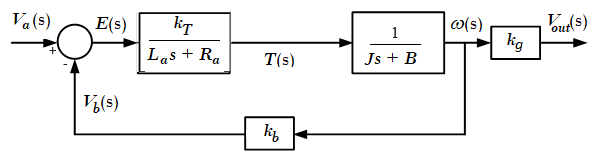
Fig. 3. Block diagram of an armature-controlled dc motor for open loop speed control
Closed loop speed control
DC motors are extensively used in many drives where speed control is desired. In many applications where a constant speed is required, open-loop operation of dc motors may not be
satisfactory. In open-loop operation, if load torque changes, the speed will change too. In a closed-loop system, the speed can be maintained constant by adjusting the motor terminal
voltage as the load torque changes.
There are other advantages of closed-loop operation, such as greater accuracy, improved dynamic response and stability of operation. In a closed-loop system the drive characteristics
can also be made to operate at constant torque or constant horsepower over a certain speed range, a requirement in traction systems. Circuit protection can also be provided
in a closed-loop system. In fact, most industrial drive systems operate as closed-loop feedback systems. The speed at the motor shaft is sensed by the tachometer with a gain kg
. The speed performance of the motor can be improved by using a proportional feedback controller. The controller is composed of a sensor (usually a tachometer for speed applications) to sense the speed
and an amplifier with gain k (proportional control). For ease in comparison of input and output, the input to the control system is converted from voltage Vin to speed ωin
using the tachometer gain kg. Hence we have
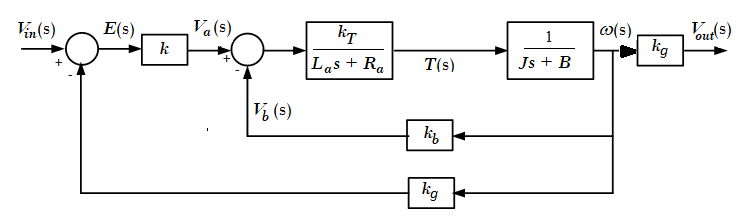
Fig. 4. Block diagram of closed loop speed control of an armature-controlled dc motor
The mathematical expression for closed loop speed control is,
$$\omega(s) = \frac{\frac{k k_T k_g}{R_a J}}{s + (\frac{k_T k_b + R_a B + k_g k_T k}{R_a J})} \omega_{in}(s) \tag 5$$
assuming La = 0
Where,
J = Moment of inertia of the motor in kg-m2
B = Viscous-friction coefficient of the motor in N-m/rad/sec
kg = Tachogenerator constant
k = Amplifier gain
kT = Motor torque constant
kb = Back emf constant
Ra = Armature resistance in Ω
La = Armature inductance in henry
Va = Applied armature voltage in volts
Closed loop position control
To control the position of the motor shaft, the simplest strategy is to use a proportional controller with gain k.
The block diagram of the closed-loop position control system is shown in Fig. 5.
The system is composed of an angular position sensor (usually an encoder or a potentiometer for position applications). For simplicity, the input voltage can be scaled
to a position input θin(s) so that the input and output have the same units and scale. Alternatively, the output can be converted into voltage using the sensor gain value. The
closed-loop transfer function in this case becomes,
$$\frac{\theta(s)}{\theta_{in}(s)} = \frac{\frac{k k_T k_s}{R_a J}}{s^2 + (\frac{R_a B + k_T k_b}{R_a J})s +\frac{k k_T k_s}{R_a J}} \tag 6$$
ks = Sensor gain
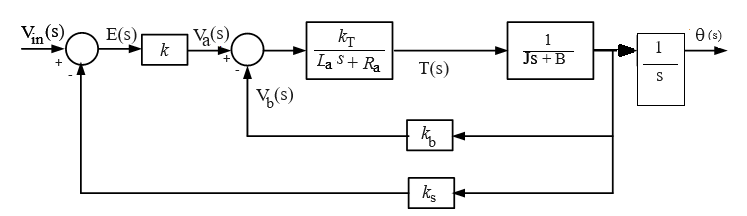
Fig. 5. Block diagram of position control of an armature-controlled dc motor
Important Equations of a dc motor
Let us consider V is the supply voltage, Eb is the back emf produced and Ia, Ra are the armature current and armature resistance respectively of a dc motor. Then the voltage equation is given by,
$$V = E_b + I_a R_a \tag 7$$
we multiply both sides of equation (7) by Ia
$$V I_a = E_b I_a + I_a^{2} R_a \tag 8$$
Now Ia2Ra is the power loss due to heating of the armature coil and the true effective mechanical power that is required to produce the desired torque of dc machine is given by,
$$p_m = E_b I_a \tag 9$$
The mechanical power pm is related to the electromagnetic torque Tg as,
$$p_m = T_g \omega \tag {10}$$
Where, ω is speed in rad/sec. Now equating equation (9) and (10) we get,
$$E_b I_a = T_g \omega \tag {11}$$
For simplifying the torque equation of dc motor we substitute.
$$E_b = \frac{P \phi Z N}{60A} \tag {12}$$
Substituting equation (12) in (11), we get:
$$T_g = \frac{P \phi Z I_a}{2\pi A} \tag {13}$$
This is the torque equation of dc motor. It can be further simplified as:
$$T_g = K_a \ \phi I_a \tag {14}$$
where,
$$K_a = \frac{PZ}{2 \pi A}$$
Where,
P is number of poles of the dc motor,
Φ is flux per pole,
Z is number of conductors of the dc motor,
A is number of parallel paths of the dc motor,
and N is the speed of the dc motor in rpm
