Crystal Field Theory
Theory
CFT was proposed by the physicist Hans Bethe in 1929. Subsequent modifications were proposed by J. H. Van Vleck in 1935 to allow for some covalency in the interactions.

Crystal Field Theory was developed to describe important properties of complexes (magnetism, absorption spectra, oxidation states, coordination,). The basis of the model is the interaction of d-orbitals of a central atom with ligands, which are considered as point charges. According to CFT, the attraction between the central metal and ligands in a complex is purely electrostatic.
The theory is developed by considering energy changes of the five degenerate d- orbitals being surrounded by an array of point charges consisting of the ligands. As a ligand approaches the metal ion, the electrons from the ligand will be closer to some of the d-orbitals and farther away from others, causing a loss of degeneracy. The electrons in the d-orbitals and those in the ligand repel each other due to repulsion between like charges. Thus, the d-electrons closer to the ligands will have a higher energy than those further away, which results in the d-orbitals splitting in energy.
This splitting is affected by the following factors:
- The nature of the ligands. The stronger the ligand, the greater is the splitting.
- Oxidation state of the central metal ion. A higher oxidation state leads to larger splitting.
- Size of d orbitals (i.e., transition series).
- Geometry of the complex.
Orbital Splitting:
The five d-orbitals are given the symbols dxy, dzx, dyz, dx2−y2, and dz2. In a complex they are all differently aligned relative to the incoming charge. Depending on the geometry of the complex, some of the d-orbitals will point directly towards the ligands, while some will point between them. Those which point at the ligands will experience more repulsion between their own electrons and those of the incoming ligands, than will those which do not point directly at them.
Thus, the orbitals pointing at the ligands will be less stable and higher in energy. Now all the d-orbitals are no longer equivalent, giving rise to the phenomenon of orbital splitting, and the difference in energy between the more and less repelled orbitals is called the crystal field splitting parameter.
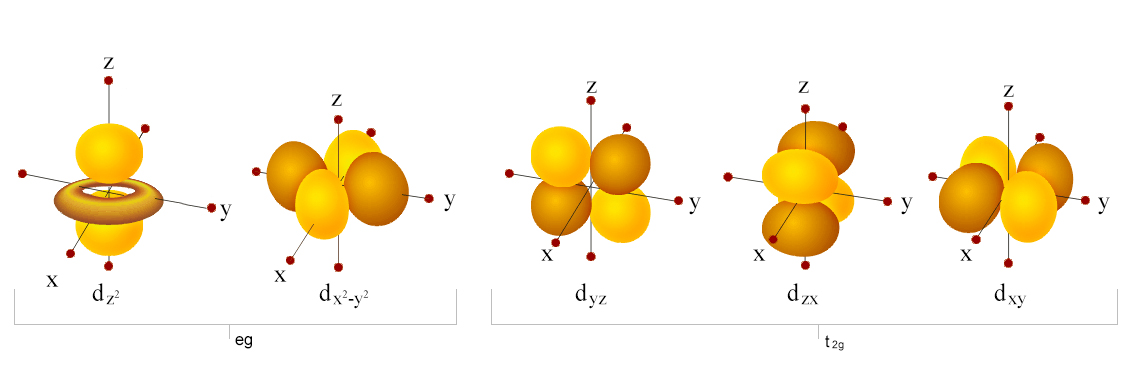
Angular dependence functions of d-orbitals
The electrons can go into either a high spin or low spin arrangement depending on the magnitude of the crystal field splitting energy.
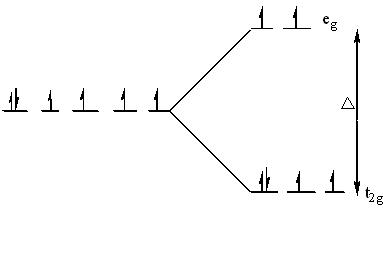
High spin
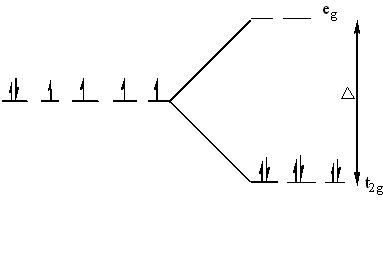
Low spin
The Spectrochemical Series:
The variation of the magnitude of the crystal field splitting (Δ) with the nature of the ligand follows a regular order, known as the spectrochemical series. This series is given below in the order in which ligands produce increasing values of Δ.
I− < Br− < S22− < SCN− < N3− < F− < urea, OH− < ox, O2− < H2O < NCS− < py, NH3 < en < bipy, phen < NO2− < CH3−, C6H5− < CN−
- Weak field ligands have small Δ and will form high spin complexes.
- Strong field ligands have large Δ and will form low spin complexes.
Octahedral Complexes:
The octahedral arrangement of six ligands surrounding the central metal ion is as shown in the figure.
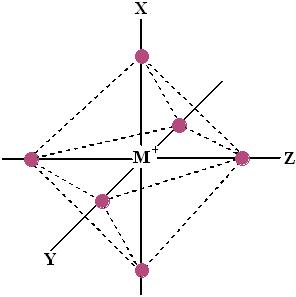
In an octahedral complex, the metal ion is at the centre and the ligands are at the six corners. In the figure, the directions x, y, and z point to the three adjacent corners of the octahedron. The lobes of the eg orbitals (dx²−y² and dz²) point along the x, y, and z axes, while the lobes of the t2g orbitals (dxy, dzx, and dyz) point in between the axes.
As a result, the approach of six ligands along the +x, +y, +z, −x, −y, and −z directions will increase the energy of the dx²−y² and dz² orbitals (which point towards the ligands) much more than it increases the energy of dxy, dzx, and dyz orbitals (which point in between the metal–ligand bond axes).
Thus, under the influence of an octahedral field, the d orbitals split into a triply degenerate set of orbitals with lower energy (t2g) and a doubly degenerate set with higher energy (eg). The average energy level between these two sets is taken as zero, which is called the barycentre. This splitting is referred to as crystal field splitting.
The magnitude of stabilization for the t2g orbitals is 0.4 Δo, and the magnitude of destabilization for the eg orbitals is 0.6 Δo.
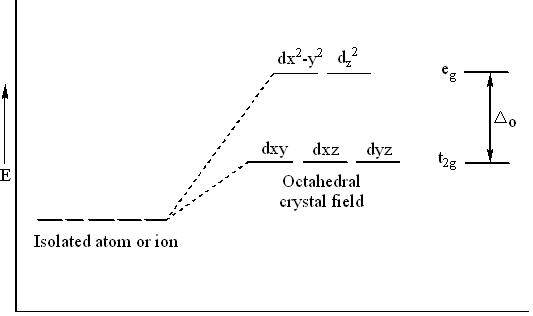
The magnitude of the splitting of the t2g and eg orbitals changes from one octahedral complex to another. It depends on the identity of the metal ion, the charge on this ion, and the nature of the ligands coordinated to the metal ion.
Tetrahedral Complex:
The tetrahedral arrangement of four ligands surrounding the metal ions is as shown in the figure.
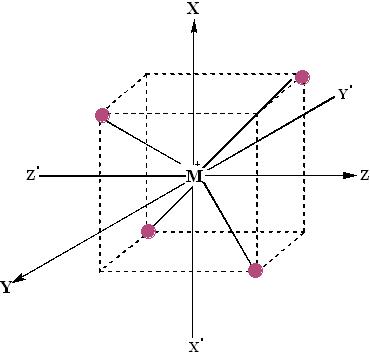
A regular tetrahedron is a cube. One atom is at the centre of the cube and four of the eight corners of the cube are occupied by ligands. The directions x, y, and z point to the face centres. The dx²−y² and dz² orbitals point along the x, y, and z directions, and the dxy, dzx, and dyz orbitals point in between the x, y, and z directions.
The direction of approach of ligands does not coincide exactly with either the e or t2 orbitals. The t2 orbitals are pointing close to the direction in which the e orbitals lie in between the ligands. As a result, the energy of t2 orbitals increases compared to the energy of e orbitals.
Thus, d orbitals again split into two sets—triply degenerate t2 orbitals of higher energy and doubly degenerate e orbitals of lower energy. That is, t2 orbitals are raised by 0.4 Δt in energy, and the e orbitals are stabilized by 0.6 Δt in energy.
The energy difference between the two sets of orbitals (Δt) will be about half the magnitude of that in an octahedral complex (Δo).
The d-orbitals will thus split as shown below:
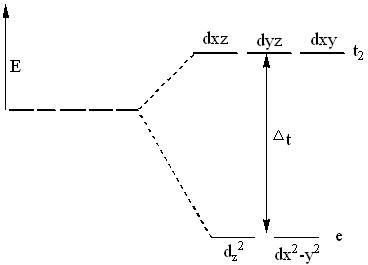
Crystal Field Stabilization Energy:
The crystal field stabilization energy (CFSE) is the stability that results from placing a transition metal ion in the crystal field generated by a set of ligands. It arises due to the fact that when the d-orbitals are split in a ligand field (as described above), some of them become lower in energy than before with respect to a spherical field known as the barycentre, in which all five d-orbitals are degenerate.
For example, in an octahedral case, the t2g set becomes lower in energy than the orbitals at the barycentre. Owing to the splitting of the d orbitals in a complex, the system gains extra stability due to the rearrangement of the d electrons filling the lower-energy orbitals.
The consequent gain in bonding energy is known as crystal field stabilization energy (CFSE).
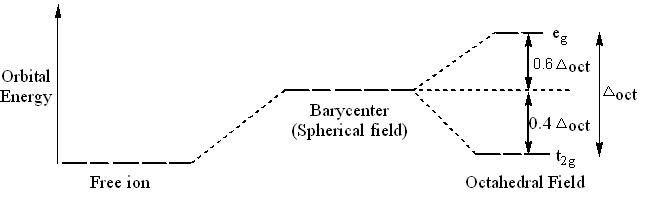
If the splitting of the d-orbitals in an octahedral field is Δoct, the three t2g orbitals are stabilized relative to the barycentre by 2⁄5 Δoct, and the eg orbitals are destabilized by 3⁄5 Δoct.
For an Octahedral Complex, CFSE:
CFSE = –0.4 × n(t2g) + 0.6 × n(eg) × Δo
Where n(t2g) and n(eg) are the number of electrons occupying the respective levels.
For a Tetrahedral Complex, CFSE:
The tetrahedral crystal field stabilization energy is calculated in the same way as the octahedral case. The magnitude of the tetrahedral splitting energy is only 4⁄9 of the octahedral splitting energy:
Δt = 4⁄9 Δo
CFSE = 0.4 × n(t2) – 0.6 × n(e) × Δt
Where n(t2) and n(e) are the number of electrons occupying the respective levels.
