Apparatus used:

Linear Air track, Air blower, two gliders, two light gates, two retort stands, velcro-pads, additional masses, data logger/acquisition system, computer system.

THEORY

This experiment is devised to familiarize with the concept of impulse, momentum and coefficient of restitution and to validate the law of conservation of linear momentum and conservation of energy as applied to collision of objects on a linear air track.

Momentum

A moving body possesses a quality which causes it to exert a force upon anything which tries to stop it. The faster an object is traveling, or the more massive it is, the more difficult it is to stop. In mechanics, this concept is termed as the linear momentum of the body. and is defined by the relation: Momentum

Where m – mass of the object v – velocity of the object Linear momentum is a vector quantity having same direction as the velocity vector, i.e. tangent to the path. For multiple objects in a system, the total momentum is a vector sum of the individual momenta

As opposed to the common convention to describe second law as ΣF=ma, Newton stated that the rate of change in the momentum of an object is directly proportional to the amount of force exerted upon the object. In mathematical terms, this differential equation can be written as:

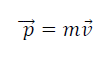
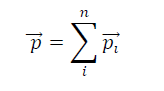
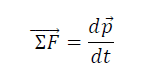
Impulse-Momentum Principle

In order to change the momentum of a particle, the resultant force should act over a period of time

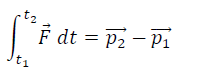
This vector on the LHS is called the linear impulse of the force F during the interval and is denoted by the term I. A more generalised form of the equation can be written as follows

This equation represents the Impulse-Momentum Principle and can be expressed in terms of impulsemomentum diagrams

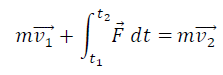
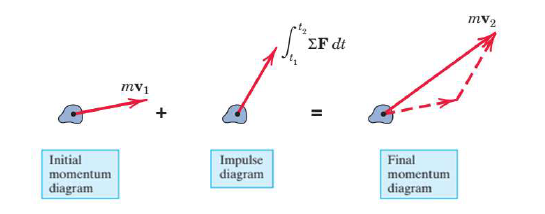
Impulse-Momentum principle is a powerful tool that can be applied for a system of particles in which the forces that act on them exerts itself for a very short duration of time (impulsive forces). A classical example of such type is the collision of bodies where the net impulse of bodies colliding is zero since the impact forces are equal and opposite. The force of gravity generally has a negligible impulse, so it does not appear in our calculations of impact. Since the effects of external impulses are very small, then the total linear momentum before impact is equal to the total linear momentum after the impact

Law of Conservation of Linear Momentum

For a closed system, the total momentum cannot change unless acted upon by an external force. In other words, the total momentum for a system of isolated bodies is constant. This general law of nature is commonly referred as the law of conservation of linear momentum. For example, consider a one-dimensional collision of two objects along a straight line. The objects with masses m1 and m2 have initial velocities v1 and v2, After collision, After the collision, the objects will have new velocities v1’ and v2’, where all velocities are assumed to be in the positive direction. Conservation of momentum demands that the total momentum must be the same before and after the collision. In other words, if the momentum of one object decreases by a certain value, the momentum of the other object increases by an equal amount.

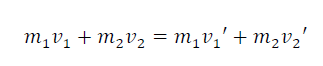
Theoretically, there are two special kinds of collisions: the perfectly elastic and perfectly inelastic collisions. While both of these processes conserve momentum, in the perfectly elastic collision the total kinetic energy, is also conserved (no loss in KE).

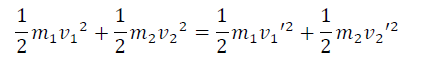
In a perfectly inelastic collision, the objects which collide and stick together. Here the kinetic energy is not conserved since some of the energy is lost into other forms

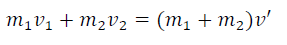
However, in most practical applications, collisions are neither perfectly elastic nor perfectly inelastic but partially elastic. This means that the impulse during the period of deformation (deformation impulse) is greater than the period of restitution (restitution impulse). In other words, the relative velocity of the colliding objects before collision is greater than that after the collision. In this case, it is valuable to define a quantity called the coefficient of restitution, a measure of the elasticity of the collision

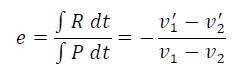
For a perfectly elastic collision, e = 1 and for a perfectly inelastic collision (starting with two bodies and ending with one), e = 0. For most real collisions, the coefficient of restitution has a value somewhere between the two extremes (0 < e < 1)

Experimental Setup

The experimental setup consists of an air track with the gliders that are subjected to collision. the An air track is a perforated rail which is connected to an air blower. Compressed air is sprayed from the holes and forms a thin layer on the surface of the track. This layer fills the space between the air track and the inner surface of a glider. As a result, the movement of the glider can be regarded as almost friction-free. The gliders have provision to attach velcro-pads on one side, which will allow the carts to stick together. They also have provision to add extra weights

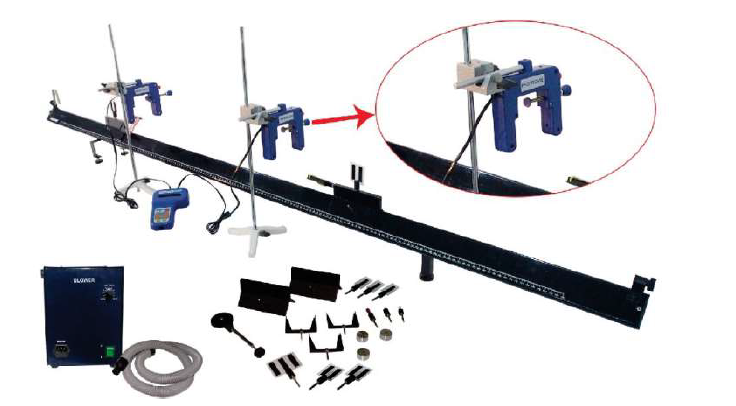
Please note that

• Do not slide the air gliders on the air-track without the air supply on
• Keep glider speeds less than 30 cm/s for best results.