Theory

When a point moves along a line that is simultaneously rotating, its absolute acceleration is the vector sum of three components:

1. The acceleration of a coincident point on the line relative to the fixed rotational center.
2. The relative acceleration of the moving point with respect to the coincident point.
3. The third component, called Coriolis component of acceleration.

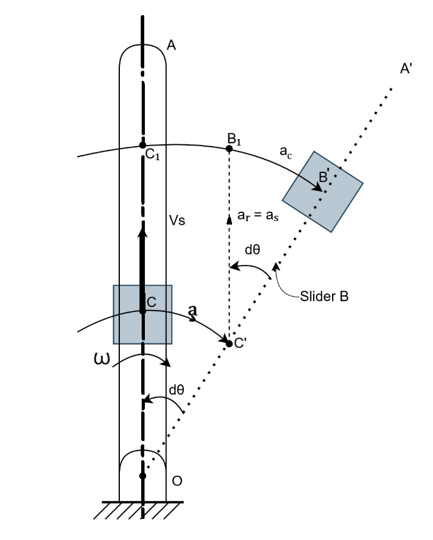
Consider a link OA which has a slider B which is free to slide, as shown in Fig. With O as centre, let the link OA move with a uniform angular velocity ω, to its new position OA' such that it is displaced dθ in time dt. The slider B moves outwards with sliding velocity v on link OA and occupies the position B' in the same interval of time.

The point C is the coincident point with slider on link OA.

The motion of slider can be explained in the following three stages:

• (i) Motion from C to C' due to rotation of link OA. It is caused by tangential component of acceleration a′.
• (ii) Motion from C' to B₁ due to outward motion along the link OA. It is caused by radial component (or sliding component aᵣ) of acceleration.
• (iii) Motion from B₁ to B' is caused by Coriolis component of acceleration a꜀.
• Therefore, from the geometry of the figure:
  Arc B₁B′ = Arc C₁B′ − Arc C₁B₁
         = OC₁(dθ) − OC(dθ)
         = (OC₁ − OC)(dθ)
         = C′B₁ × dθ .....(i)
  
  We know that: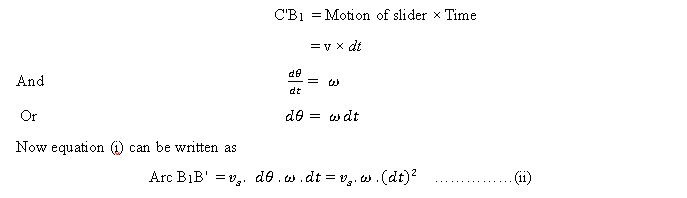

  

Considering constant acceleration of slider:

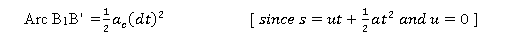
For small θ,

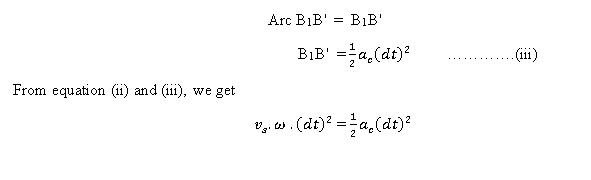
Hence,
Coriolis component of acceleration:

Where,

• a꜀ = Coriolis component of acceleration in m/sec²
• v = velocity of sliding in m/sec
• ω = angular velocity in rad/sec of link OA

---

Hydraulic Analogy

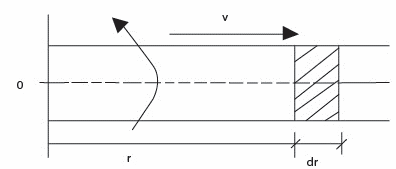
Consider a short column of fluid of length dr at radius r from axis of rotation of the tube.
If velocity of fluid relative to tube is v, and angular velocity of tube is ω, then Coriolis component of acceleration is 2ωv.

For a fluid column of length dr at radius r:

Force:

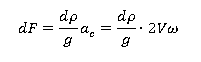
Torque:

Here, ⅆρ is the weight of the fluid element: ⅆρ= ρa dr

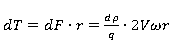
Where:

• p = specific weight (N/m³)
• a = cross-sectional area (m²)

In a direction perpendicular to rotation of tube.

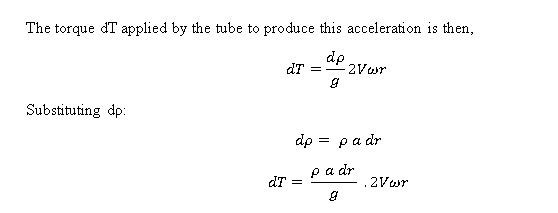
Total Torque Integration:
Integrate from r = 0 to r = L (effective tube length):

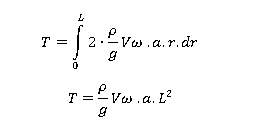
Rearrange the torque equation to solve for a꜀: Hence, Coriolis component of acceleration,

---

Apparatus

The apparatus uses hydraulic analogy to determine Coriolis' component of acceleration.
It consists of two brass tubes connected to a central rotor distributor. The distributor is rotated by a variable-speed D.C. motor. Water is supplied to the distributor by a pump through a rotameter.
When tubes are rotating with water flowing through them, and with various measurements provided, Coriolis’ component can be determined both experimentally and theoretically.

---

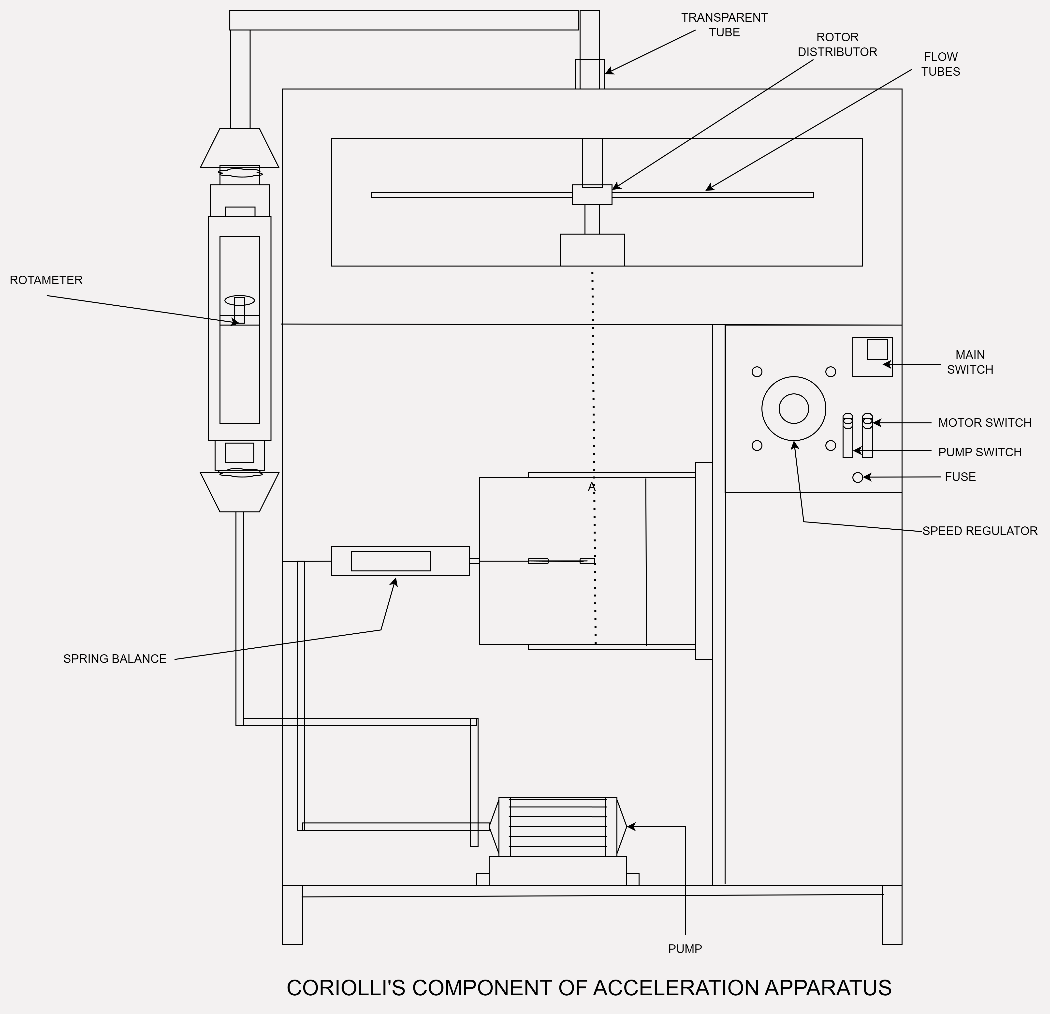
Specifications

1. Pipes – 8 mm I.D, 312 mm effective length – 2 Nos.
2. Drive motor – 0.5 HP, 1500 RPM D.C. motor, swinging field type with speed control.
3. Torque arm radius – 0.112 m with 5 kg capacity spring balance.
4. Pump – 0.5 HP capacity, 25 × 25 mm connection, single phase.
5. Rotameter
6. Housing – for rotating pipes, which also acts as water reservoir, with top Perspex sheet.