Tools

Clipping: Line

Cohen Sutherland's Line Clipping Algorithm

  • The Cohen–Sutherland algorithm is a line clipping algorithm used in computer graphics. After dividing a 2D space into 9 regions, the algorithm effectively identifies the lines and line segments that are visible in the viewport, which is the center region of interest.
  • The division of regions is based on a window defined by its maximum (xmax, ymax) and minimum (xmin, ymin) coordinates. One region represents the window itself, while the other 8 regions surround it, identified using a 4-digit binary code.

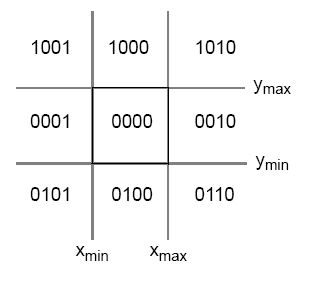
Region Codes Assignment

  • Each endpoint of a line segment is assigned a 4-bit binary region code based on its position relative to the clipping window:
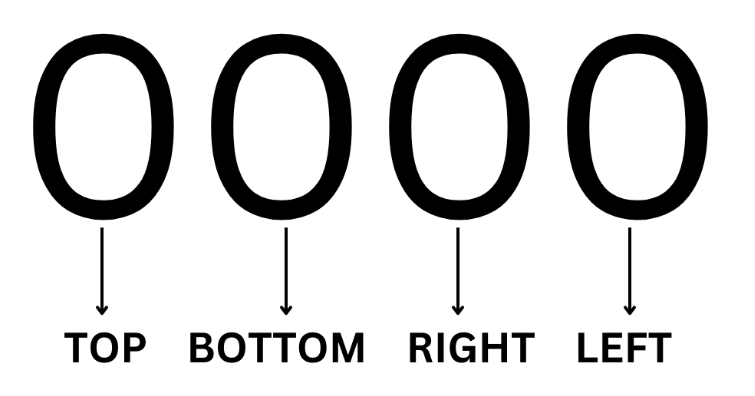
    • Bit-1 (Top): 1 if y > ymax , 0 otherwise.
    • Bit-2 (Bottom): 1 if y < ymin , 0 otherwise.
    • Bit-3 (Right): 1 if x > xmax , 0 otherwise.
    • Bit-4 (Left): 1 if x < xmin , 0 otherwise.

For example:

  • If a point (x, y) lies in top-right of the clipping window, its region code will be 1010.

Trivial Acceptance and Rejection:

  • If both endpoints have a region code of 0000, the line segment is completely inside the clipping window and can be accepted.
  • If the bitwise AND of both codes is not 0000, the line segment is completely outside and can be rejected.

Line Clipping Algorithm Pseudo Code

  1. Assign region codes to both endpoints points (A(x1, y1) and B(x2, y2)) of the line segment.

  2. Perform a bitwise OR operation on both endpoints:

    • If OR == 0000,
      • The line is completely inside the window (Trivially accepted).
    • Else,
      • Perform a bitwise AND operation on both endpoints:
        • If AND != 0000,
          • The line is not inside the window, it cannot be clipped (Trivially rejected).
        • Else,
          • The line is partially inside the window and can be considered for clipping.

  3. After confirming the line is partially inside the window:

    • Find the intersection with the boundary of the window:
      • Calculate the slope of the line: m = (y2 - y1) / (x2 - x1).
      • Determine the intersection point based on the region code:
        • If the line intersects with the top boundary:
          • x = x1 + (1 / m) * (ymax - y1)
          • Update the intersection point (x, ymax)
        • If the line intersects with the bottom boundary:
          • x = x1 + (1 / m) * (ymin - y1)
          • Update the intersection point (x, ymin)
        • If the line intersects with the left boundary:
          • y = y1 + m * (xmin - x1)
          • Update the intersection point (xmin, y)
        • If the line intersects with the right boundary:
          • y = y1 + m * (xmax - x1)
          • Update the intersection point (xmax, y)

  4. Overwrite the endpoint with the new intersection point and update its region code.

  5. Repeat step 2-4 until a trivial accept or reject occurs.

  6. Repeat the entire process for other lines as needed.


  • This pseudo code outlines the steps of the Cohen–Sutherland line clipping algorithm, detailing how line segments are processed and clipped against a defined clipping window in 2D space.