Carey Foster's Bridge to Measure Specific Resistance of Material
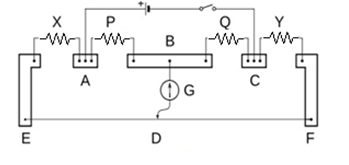
The Carey Foster’s bridge is as in the figure1. One meter long wire of manganin (Specific Resistance = 43x 10-6 ohm -cm) or constantan (Specific Resistance = 40 x 10-6 ohm -cm) of uniform cross-section area is stretched along a meter scale. The wire is connected at both the ends with copper strips. Beside these strips there is one copper strip B fixed parallel to the meter scale and two L-shaped strips A and C at the ends of the scale. In between these strips there are four empty spaces AB, CD, EF and GH. In first empty space AB known resistance X, in second empty space CD a resistance P, in third empty space a resistance Q and in fourth empty space GH the known resistance Y is connected. The Leclanche cell E and plug key K are connected in between A and C. Between the points B and D, galvanometer G is connected. At point D, contact key is fixed which can move here and there on the wire EF. This key is known as jockey. On pressing jockey, point D gets connected with the galvanometer otherwise not.
Formula Used:
- Resistance per unit length of the wire of bridge
ρ = X/ (l2-l1) ohm/cm----- (1)
Where l1 = balancing length on the bridge wire measured from the left end when known resistance X is connected in left gap of the bridge and zero resistance is connected in right gap of the bridge and l2 = balancing length of the bridge wire measured from the left end on interchanging the positions of X and Y.
- Unknown resistance of the given wire
Y = X – (l2 – l1) ρ----- (2)
where X = unknown resistance connected in the left gap, Y = resistance of the wire connected in the left gap, l1 and l2 respectively are the balancing lengths of the bridge wire measured from the left end, before and after interchanging the positions of X and Y.
Specific resistance of the given wire:
Ks = (πr2/l) Y ----- (3)
Where r is the radius and l is the length of the given wire. Value of both the parameters is provided to the student.