Vib-rotational Spectroscopy of Carbon dioxide
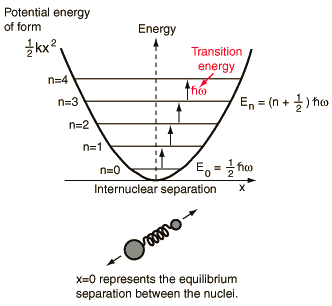
The vibrational transitions of a diatomic molecule in its electronic ground state can be approximated to a Simple Harmonic Oscillator (SHM). The rotational transitions can be approximated to a rigid rotor.
In this lab, please distinguish between ν(spelled 'nu') and v(alphabet 'v'). While the ν is used to denote the frequency, the symbol v denotes the vibrational quantum number.
Selection
For vibrational transitions: The molecule should have a dipole moment. Δv=±1,±2,.., where v is the vibrational quantum number.
For rotational transitions: ΔJ=±1, where J is the rotational quantum number.
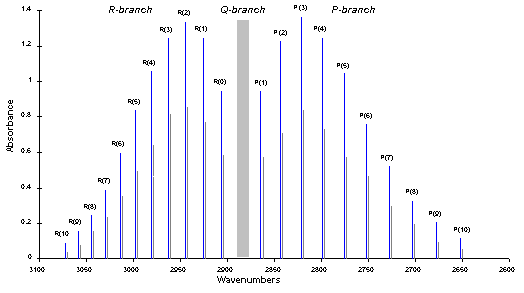
Spectrum identification
- The P-branch corresponds to all transitions where ΔJ=−1
- The R-branch corresponds to all transitions where ΔJ=+1
- The Q-branch corresponds to all transitions where ΔJ=0
Calculation of Bond force constant
Calculation of Bond length
The rotational energy is given by
