Bubble Sort
Demonstration of Optimized Bubble Sort Concept
Optimization Technique
Now that we have seen and understood how Bubble Sort works, let's take note of a few observations :
- As we pointed out before, after the Tth iteration, the Tth largest element is placed correctly (at the Tth index from the end).
- Given this fact, we can say that if we're on the Tth iteration, the greatest (T-1) elements already occupy their correct places among the last (T-1) indices of the array.
- Hence, we don't have to compare these elements again and again in subsequent iterations. Instead, in the Tth iteration, we can just compare the first (N-T+1) elements.
- Since we are reducing the number of redundant comparisons, the running time of the algorithm will be lesser.
When can we Stop?
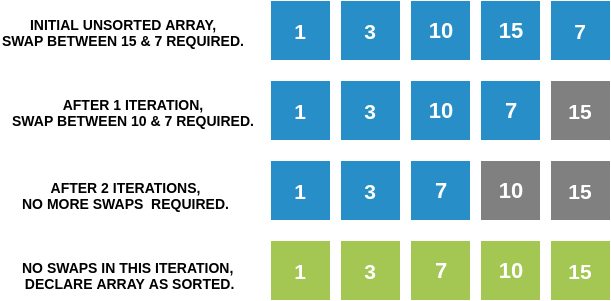
- In many cases, we notice that the array gets sorted much before the N iterations are completed.
- To avoid redundant iterations, we can check whether or not our array is sorted, after each iteration. We can terminate our algorithm if the array is sorted.
- How do we check if our array is sorted? Notice that if we run an iteration where no swaps are required, it means that all pairs of adjacent elements are correctly ordered, or in other words, the array is sorted.
- Hence, whenever we encounter one full iteration without any swaps, we can safely declare the array as sorted.
- Note that given an already sorted array, we will be able to terminate our algorithm in one iteration itself.
Visualization of Optimized Bubble Sort

When to Stop?