Binary Search Tree
Relationships of Binary Search Trees (BST)
A Binary Search Tree (BST) is a special type of binary tree that maintains a specific order among its elements, enabling efficient search, insertion, and deletion operations.
BST vs. Arrays
- Arrays store elements in contiguous memory locations and allow direct access by index, but searching for a value in an unsorted array requires linear time (O(n)).
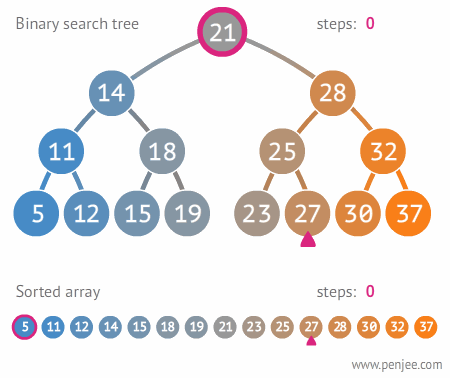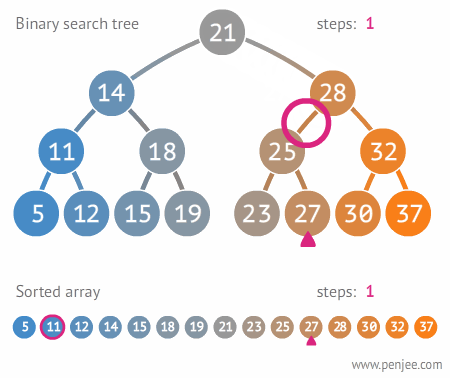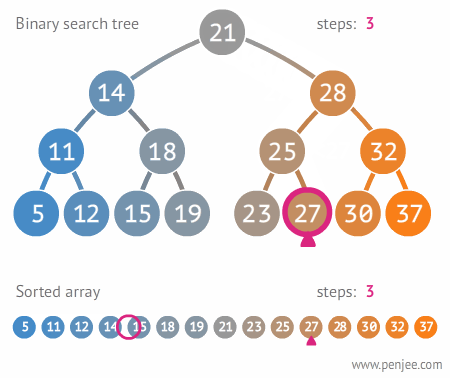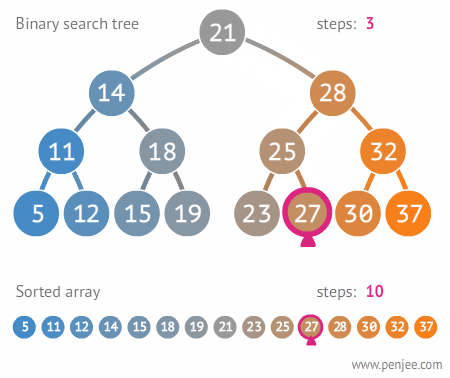
- Sorted arrays allow binary search (O(log n)), but insertion and deletion are costly (O(n)) due to shifting elements.
- BSTs allow dynamic insertion and deletion in O(h) time (where h is the height of the tree), and searching is also O(h). In a balanced BST, h = O(log n).
- Traversal: An in-order traversal of a BST yields the elements in sorted order, similar to a sorted array.
BST vs. Linked Lists
- Linked lists provide efficient insertions and deletions at any position (O(1) if the node is known), but searching is linear (O(n)).
- BSTs combine the benefits of dynamic insertion/deletion with faster search (O(h)), provided the tree remains balanced.
- A degenerate (unbalanced) BST can become a linked list, losing its efficiency.
BST vs. Other Trees
- Heaps: Heaps are binary trees used for priority queues, maintaining a different order property (parent is greater/less than children). Heaps do not support efficient searching for arbitrary elements.
- AVL Trees, Red-Black Trees: These are self-balancing BSTs that guarantee O(log n) height, ensuring consistently fast operations.
- B-Trees: Used in databases and filesystems, B-Trees generalize BSTs to allow more than two children and keep data balanced for efficient disk access.
Traversal Comparisons
- In-order Traversal (BST): Visits nodes in ascending order (left, root, right).
- Pre-order/Post-order Traversal: Useful for copying or deleting trees, not for sorted order.
- Level-order Traversal: Visits nodes level by level, similar to breadth-first search.
Visual Example