Binary-input Memoryless Channels
What is a Communication Channel?
A communication channel is a medium through which communication happens. In this virtual lab, we are dealing with specifically those channels that accept binary-valued inputs. We call these channels as binary-input channels. For some binary channels, we write the possible set of inputs as the logical bits . That is, at any time instant, we can send a logical "0" through the channel, or a logical "1". Equivalently, we may also write the binary alphabet in the bipolar form, which is written as . Normally, we take the logical-bit to bipolar mapping as and .
We generally use the notation to denote the input alphabet of the channel. From the point of view of the receiver, the input to the channel is unknown, and hence is modelled as a random variable with some input probability distribution. We denote this input random variable as . Similarly, the output of the channel, is a random variable denoted by . We assume that the output alphabet, the set of all values that the output can possibly take, is denoted by .
Types of Channels considered in this virtual lab
The problem of designing good communication systems arises precisely due to the existence of noise in communication channels. The noise in the communication channel is generally modelled via the conditional probabilities (of the output value, given the input value). We consider some three important types of communication channels (or in other words, noise models) in this virtual lab.
- The Binary Erasure Channel: The noise in this channel is modelled as a bit-erasure, which denotes the transmitted bit was erased or lost. Formally, in this channel, the input alphabet is the set of logical bits, i.e., and the output alphabet is the set of logical bits along with the erasure symbol , i.e., . The erasure symbol denotes that the input symbol was erased during the process of transmission through the channel. The binary erasure channel, denoted formally as , has the property that the bit that is transmitted is erased with probability . Here, denotes the erasure probability, and we assume is a real number between and , i.e., .
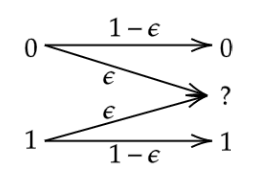
Depiction of a Binary Erasure Channel. The left side denotes the possible inputs {0,1} and the right denotes the possible outputs {0,1,ϵ} . The arrows indicate possible transitions when the bit passes through the channel. The values ϵ, (1-ϵ) marked upon the respective arrows indicates the probability of such a transition.
- The Binary Symmetric Channel: In this channel, the input alphabet is the set of logical bits, i.e., and the output alphabet is the set of logical bits i.e., . The noise of this channel is characterized by bit-flips (i.e., a transmitted bit is received as a , or vice-versa). In the binary symmetric channel denoted by , we assume that bit-flip happens with some probability , where is a real number and .
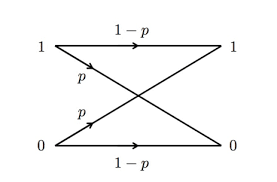
Depiction of a Binary Symmetric Channel. The left side denotes the possible inputs {0,1} and the right denotes the possible outputs {0,1}. The arrows indicate possible transitions when the bit passes through the channel. The values p, (1-p) marked upon the respective arrows indicates the probability of such a transition.
- The Additive White Gaussian Noise Channel (AWGN): The AWGN channel, accepts a real number as an input, and adds to it a noise random variable that is distributed independently according to a Gaussian distribution , with zero-mean and variance . Thus, the input alphabet and the output alphabet are both . The relationship between the input and the output is then given as
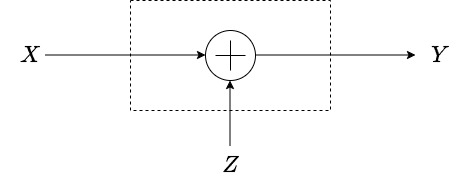
Depiction of a Additive White Gaussian Noise Channel. The left side denotes the possible input X and the right denotes the possible output Y. The arrows indicate the input X getting added to a noise Z to give the output Y.
Conditional Distribution Associated with the Communication Channel
We can also describe the channels above using the conditional distribution of the output random variable given by the input random variable . Specifically, we have the following.
- Binary Erasure Channel: The conditional distribution of this channel is given as follows.
- Binary Symmetric Channel: The conditional distribution of this channel is given as follows.
- AWGN Channel: For this channel, we have
The Memoryless Property of the Channels
We assume that the three channels we have considered in this virtual lab have the memoryless property and exist without feedback. To be precise, if we transmit a -length sequence of bits denoted by through any of these channels, the output is a sequence of bits , with probability as follows.
The above property is a naturally expected property. For instance, consider the channel . The probability of receiving when transmitting is given by
More generally, we can say the following. Let be an -length binary vector. A vector is said to be compatible with if and agree (i.e., are equal) in all positions which are unerased (not equal to "?" symbol) in . Otherwise, they are not compatible. For instance, the vectors and are compatible. However, the vectors and are not compatible, since the third bits of the two vectors are both unerased and not equal.
For any vector , let denote the number of erased symbols in . Then for any , we have, in the memoryless channel, the following to be true.
Turning our focus to the , we have the following. For any , let denote the Hamming distance (number of positions where and have distinct values). For example, as the two vectors are distinct in the first and the fourth locations. Then, for the memoryless channel, we have the following.
For the memoryless AWGN channel, we have, for any two vectors ,
