Infinite and Finite Well and other SWE solutions
Question 1: How many nodes (just like nodes in windpipe ) will you see in the solution for quantum number =5 inside infinite well?
?
Question 2:
Between n=2 and n=4 energy level for which quantum number will be higher?
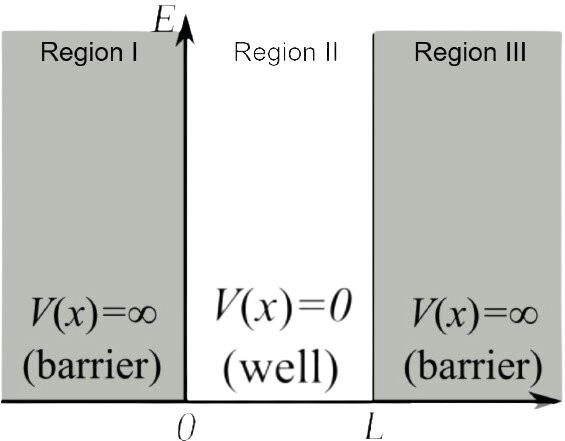 In an infinite potential well, the potential
V(x) is zero inside the well and infinite outside, confining the particle strictly within a width
L. And the probability of finding electrons at infinite potential is 0.
In an infinite potential well, the potential
V(x) is zero inside the well and infinite outside, confining the particle strictly within a width
L. And the probability of finding electrons at infinite potential is 0.
Case -1 Visualization of ψ(x) in an Infinite Potential Well
Input quantum number n (allowed values n>=0 and n<=6).
solution for different n
x-axis : distance
y-axis : energy
Question 1: What is the nature of particle wave in Region 1 ?
Question 2:
Which of these is untrue about ψ at x=0 (boundary of well wall)?
Case - 2 Visualization of ψ(x) in a finite Potential Well
Input the value of n

