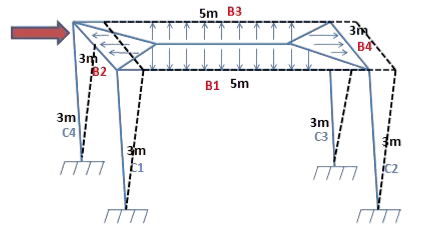
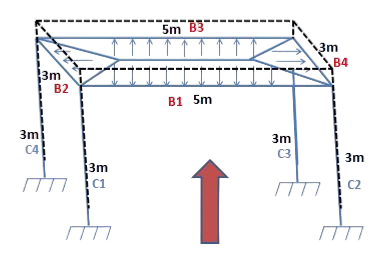
Break down 3D framed structure into 2D frames
Objective:
This experiment aims to carry out simplified load calculation and structural analysis of a 3D frame structure by breaking down into 2D frames. It deals with computation of dead loads (slabs and finish, beam and columns), imposed (live) loads & earthquake loads.
Measurement of Slab
Thickness of Slab = 0.15m
Measurements of Beam
Width = 0.3m
Depth (Thickness) = 0.3m
Length = B1 = B3 = 5m, B2 = B4 = 3m
Measurements of Columns
Length = 3.5m
Width = 0.4m
Thickness = 0.4m
Note: Please keep paper, pen and calculator with you while performing the simulation.

Dead Load of the slab = thickness x 25 = 0.15 x 25 = 3.75kN/m2
Dead load on 50mm (thickness) floor finish = 0.05 x unit weight of PCC = 0.05 x 24 = 0.36 kN/m2
1. Total Dead Load Intensity
[ + ] =
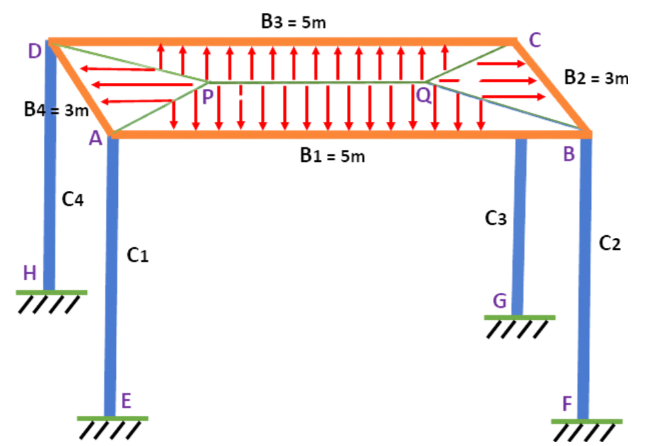
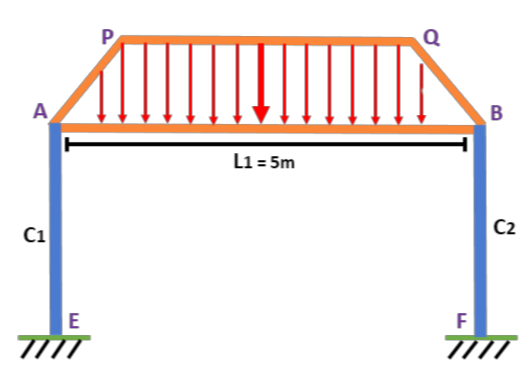
2. Now load of trapezoidal portion of the slab (APQB) acting on beam B1
Area of the trapezoidal portion x Total DL intensity
[ x ] =
Similarly DL of slab DPQC acting on Beam B3 = 21.75 kN
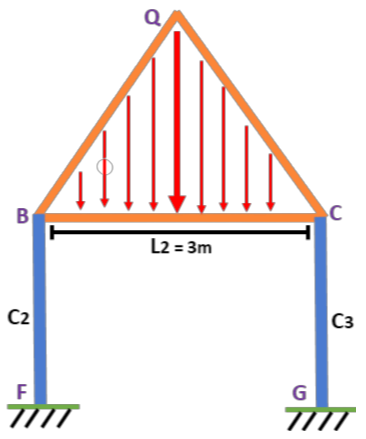
3. Now load of triangular portion of the slab (BQC) acting on beam B2
Area of the triangular portion x Total DL intensity
[ x ] =
Similarly DL of slab (BQD) acting on Beam B4 = 9.24 kN
Total Dead load of the slab = 61.62
Now, Imposed Load = 3kN/m2
Therefore, the imposed load transfered to the beams
B1 = B2 = B3 = B4 =
Also, Total IL (Live load) of slab =

Self weight of beam B1 = Volume (L1 x Width x Thickness) x Density of concrete.
[ x x ] x 25 =
Similarly the self weight of beam B3 =
Self weight of Beam B2 = Volume (L2 x Width x Thickness) x Density of concrete.
[ x x ] x 25 =
Similarly the self weight of beam B4 =
Now, Total DL of the Slab + Beams (B1, B2, B3, B4) = 97.63 kN
Calculation of self weight of columnsSelf weight of the column C1 = Volume (lc x width x thickness) x 25.
[ 3.5 x 0.4 x 0.4 ] x 25 = 14kN
Similarly the self weight of column C2 = C3 = C4 = 14 kN. ]
Now Calculate the total load transfered to the footing of each column$$ = \left(\frac{1}{4} \text{ total weight of slab}\right) + \frac{\text{self weight of beam B1 + B2}}{2} + \text{C1}$$
Total imposed load (IL) on footing = 1/4 of IL on slab = 45/ 4 = 11.25 kN

Horizontal seismic cofficient (AH) =
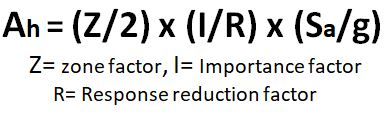
Ah =