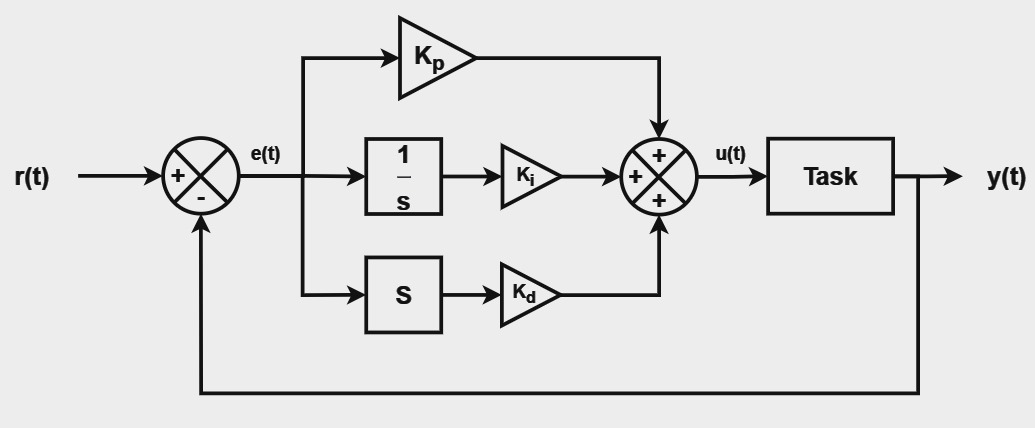
PID Feedback System
Instructions
To visualize the s-plane plot of a PID controller, follow these steps:
- Enter value for kp (proportional constant)
- Enter value for ki (integral constant)
- Enter value for kd (differential constant)
- Click on the "Plot" button to visualise the s-plane plot for the PID controller
Proportional: (kp)
Integral: (ki)
Differential: (kd)
Observations
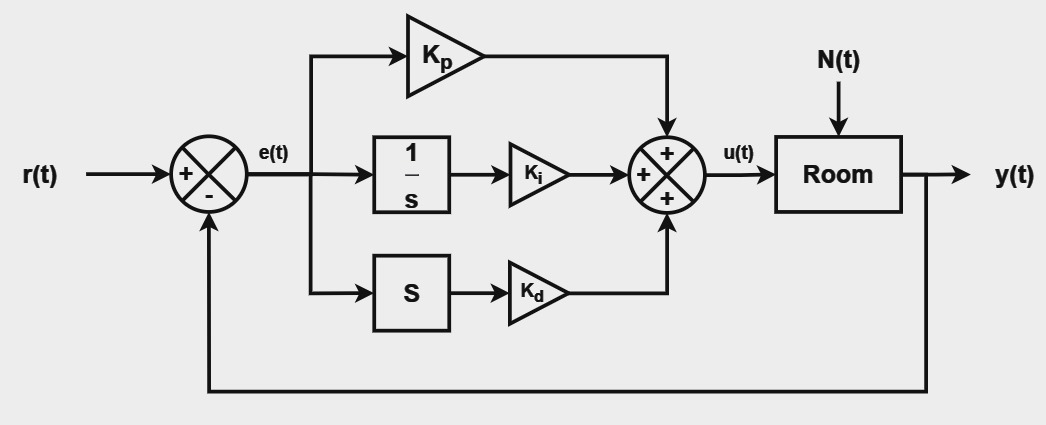
PID Temperature Controller
Instructions
To visualize the time dynamics of a PID controlled temperature controller, follow these steps:
- Enter value for current temperature (start temperature for the controller)
- Enter value for set temperature (target temperature for the controller)
- Enter value for kp (proportional constant)
- Enter value for ki (integral constant)
- Enter value for kd (differential constant)
- Click on the "Plot" button to visualise a live simulation and plotting of the time dynamics of a PID controlled temperature controller
Current Temperature
Set Temperature
Proportional: (kp)
Integral: (ki)
Differential: (kd)
Noise Level:
Observations
System Builder
Instructions
Build a system: C1·a^n·u(n) + C2·b^n·u(n).
- Enter values for C1, C2, a, b.
- Click "Simulate System" to see stability results.
C1
C2
a
b
Observations
System Stability Quiz
Instructions
Given the following impulse response of the system, determine if it's stable or not.
(a + ib)^n u(n) + (c + id)^n u(n)
- Click "Generate System" to get random parameters.
- Check if the system is stable or not.
- Click "Check Stability" to verify your answer and see the response.
a
b
c
d
Is the system stable?
Observations
Second-Order System Simulator
Instructions
Simulate a second-order system under a unit step input:
y''(t) + 2ζωn·y'(t) + ωn²·y(t) = ωn²
- Enter values for damping ratio (z) and natural frequency (wn).
- Click "Simulate" to see the step response and stability status.
ζ (Damping Ratio)
ωn (Natural Frequency)
Observations
Second-Order System Stability Quiz
Instructions
Determine if the given second-order system is stable:
y''(t) + 2ζωn·y'(t) + ωn²·y(t) = ωn²
- Click "Generate System" to get random parameters.
- Check if the system is stable or not.
- Click "Check Stability" to verify your answer and see the step response.
ζ (Damping Ratio)
ωn (Natural Frequency)
Is the system stable?
Observations
Is the System Stable? Give the poles
Instructions
- Select if the system given in the figure with the provided constants (in blue below) is stable or not
- Enter the poles separated with commas
- Truncate the values to 2 decimal places, i.e., 2.348 should be 2.34
- Click on the "Check" button to verify your answer and get feedback observations on the right
Is the system stable?
Fill the poles
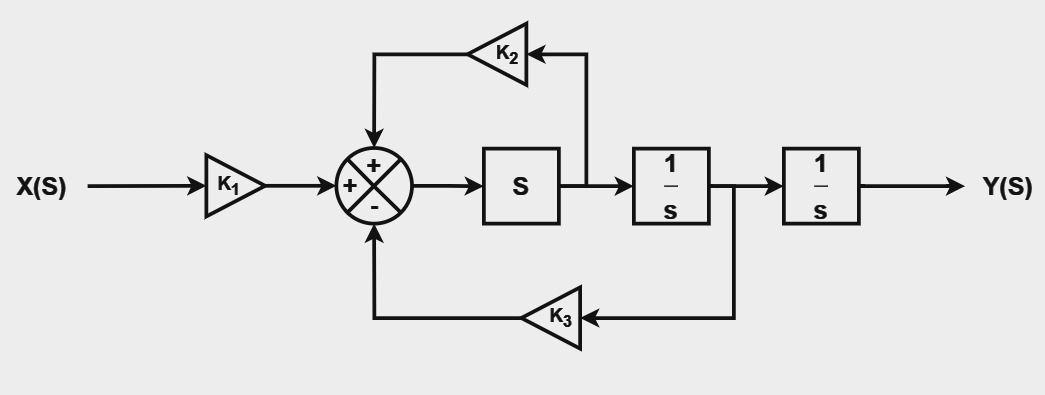
Observations
Reach within 100sec
Instructions
- Enter value for kp (proportional constant)
- Enter value for ki (integral constant)
- Enter value for kd (differential constant)
- For the given current temperature, you are expected to reach the given set temperature within 100 seconds
- Click on the "Simulate & Check" button to see a live simulation and verify your answer and get feedback observations on the right
Current Temperature 10
Set Temperature 30
Proportional: (kp)
Integral: (ki)
Differential: (kd)

Observations