Phase Modulation (PM)

Theory :

Phase modulation (PM) is a modulation technique where the phase of a carrier wave is varied according to the instantaneous amplitude of the modulating signal \( m(t) \). Unlike frequency modulation, where the frequency of the carrier is altered, in PM, the phase of the carrier signal is shifted. The modulated signal can be mathematically expressed as:

\( S(t) = A_c \cos\left[ 2\pi f_c t + K_p m(t) \right] \)

Where:

• \( A_c \) is the amplitude of the carrier signal.
• \( f_c \) is the carrier frequency.
• \( K_p \) is the phase sensitivity of the modulator, which determines how much the phase of the carrier is shifted in response to the modulating signal.
• \( m(t) \) is the modulating (baseband) signal.

In phase modulation, the phase of the carrier signal \( \cos\left[ 2\pi f_c t \right] \) is shifted by an amount proportional to the modulating signal \( m(t) \), scaled by the phase sensitivity \( K_p \). The amount of phase shift is directly proportional to the amplitude of the modulating signal.

Block Diagram:

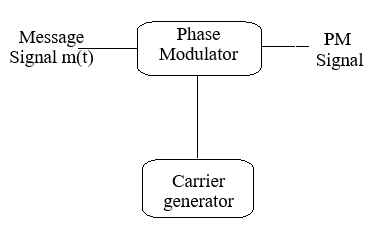
Fig: Phase Modulation

Modulation Index (Δφ) in Phase Modulation

In Phase Modulation (PM), the modulation index, denoted as Δφ (or sometimes m_p), represents the maximum phase shift of the carrier wave in response to the modulating signal.

It is defined by the peak phase deviation of the carrier:
Δφ = K_p A_m
where:

• Δφ = Peak phase deviation, measured in radians.
• A_m = The peak amplitude of the message signal m(t).
• K_p = The phase sensitivity of the modulator (in radians per volt).

The value of Δφ determines the nature of the PM signal, similar to FM:

• Δφ << 1 (typically Δφ < 0.3): Narrowband PM (NBPM). Its characteristics are very similar to AM.
• Δφ ≥ 1: Wideband PM (WBPM). This offers improved noise immunity over NBPM.

Frequency Domain Description:

A Phase Modulated (PM) signal, when modulated by a single sinusoidal tone, generates a theoretically infinite number of sidebands. These sidebands are spaced at integer multiples of the modulating frequency (ω_m) symmetrically around the carrier frequency (ω_c).

Where:

• J_n(Δφ): This is the Bessel function of the first kind of order n. Its argument, Δφ, is the phase modulation index. The value of this function determines the amplitude of the nth sideband pair.
• δ(·): The Dirac delta function, which represents the discrete spectral lines located at specific frequencies.
• ω_c: The angular frequency of the carrier signal (in rad/s).
• ω_m: The angular frequency of the modulating message signal (in rad/s).
• n: An integer (..., -2, -1, 0, 1, 2, ...) that denotes the order of the sideband.

The sidebands appear at frequencies of ω_c ± nω_m. The spectral structure is very similar to that of a Frequency Modulated (FM) signal, with the key difference being how the modulation index is defined. In PM, the modulation index Δφ is directly proportional to the amplitude of the modulating signal.

Phase Demodulation

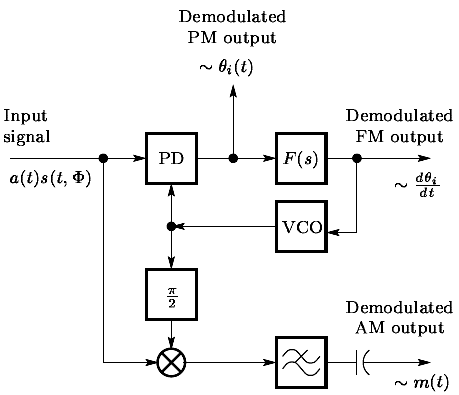
Fig : Phase Demodulation

The diagram shows a Phase-Locked Loop (PLL) used to demodulate a Phase Modulated (PM) signal. In PM, the message is encoded in the signal’s phase.

The PLL's job is to perfectly follow the phase of the PM signal. The voltage signal it creates to do this tracking is the original message.

• Phase Detector (PD): This block compares the phase of the incoming PM signal with the VCO's signal and produces an error voltage proportional to their phase difference. This phase difference varies in time according to the original message.


• Loop Filter and VCO: The loop filter smooths the error voltage, and the VCO uses it to track the phase of the incoming signal. This ensures a stable reference for accurate demodulation.

The Final Output: The output of the loop filter represents the original message signal.