Frequency Modulation (FM)

Theory :

Frequency modulation (FM) is the process where the frequency of a carrier wave, denoted as \( c(t) \), is varied in accordance with the instantaneous amplitude of the modulating signal \( m(t) \). Unlike amplitude modulation, where the amplitude of the carrier wave is varied, in FM, the amplitude remains constant while the frequency changes. The modulated signal can be mathematically expressed as:

\( S(t) = A_c \cos\left[ 2\pi f_c t + 2\pi K_f \int m(\tau) d\tau \right] \)

Where:

• \( A_c \) is the amplitude of the carrier signal.
• \( f_c \) is the carrier frequency.
• \( K_f \) is the frequency sensitivity of the modulator, defining how much the frequency of the carrier varies with the modulating signal.
• \( m(t) \) is the modulating (baseband) signal.
• \( \int m(\tau) d\tau \) represents the integral of the modulating signal, which determines the frequency deviation.

This expression shows that the instantaneous frequency of the carrier wave is proportional to the amplitude of the modulating signal. The carrier frequency \( f_c \) is shifted by an amount proportional to the modulating signal \( m(t) \), and this shift results in a frequency-modulated signal.

Block Diagram

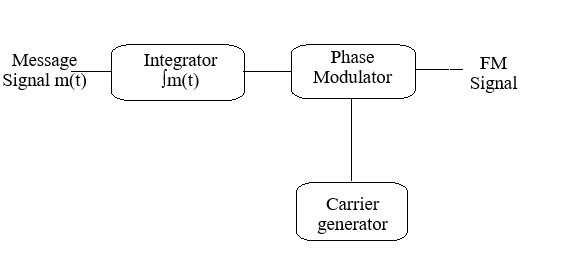
Fig: Frequency Modulation

Modulation Index (β) in Frequency Modulation

In Frequency Modulation, the modulation index, denoted by β, represents the relationship between the frequency deviation and the frequency of the modulating signal. Unlike in AM, it's not a simple ratio of amplitudes.

It is defined as the ratio of the peak frequency deviation to the modulating frequency:
β = Δf / f_m
where:

• Δf = Peak frequency deviation. This is the maximum shift in the carrier's frequency from its resting state (f_c). It is determined by Δf = K_f A_m.
• f_m = The maximum frequency of the message signal m(t).
• K_f = The frequency sensitivity of the modulator (in Hz/Volt).
• A_m = The peak amplitude of the message signal.

The value of β distinguishes between two main classes of FM:

• β << 1 (typically β < 0.3): Narrowband FM (NBFM). Its properties are similar to AM.
• β > 1: Wideband FM (WBFM). This is used in broadcasting for high-fidelity audio, as it offers superior noise immunity.

Frequency Domain Description:

An FM signal produces an infinite number of sidebands spaced at intervals of ω_m from the carrier ω_c, both above and below.

S(jω) = ∑_n=-∞^∞ J_n(β) · δ(jω - ω_c - n ω_m)

Where:

• J_n(β): Bessel function of the first kind of order n
• δ(·): Dirac delta (impulse) at each spectral line
• ω_c: Carrier angular frequency (rad/s)
• ω_m: Message angular frequency (rad/s)

Frequency Demodulation

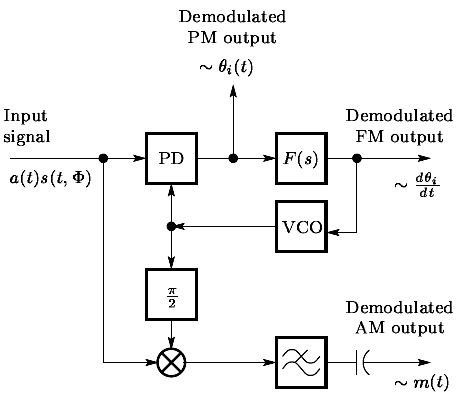
Fig: Frequency Demodulation using a PLL

The diagram shows a Phase-Locked Loop (PLL), a clever circuit for demodulating an FM signal. Think of it as a "tracking" system that tracks the frequency changes of the FM signal. The voltage used to control this tracking contains the original message.

• Phase Detector (PD): This block acts like a comparator. It looks at the incoming FM signal and the signal from the VCO and produces a "difference" or "error" voltage. If the two signals are out of sync, this voltage tells the system how to correct itself.


• Loop Filter: This cleans up the error voltage from the Phase Detector, smoothing it out and removing any unwanted noise or sudden jumps. This ensures the tracking process is stable and accurate.


• Voltage Controlled Oscillator (VCO): This is a frequency generator that is controlled by voltage. It takes the smooth error voltage from the filter as its input. This voltage tells the VCO to either speed up or slow down its frequency to perfectly match the frequency of the incoming FM signal.

The Final Output: The signal that tells the VCO what to do is the message we want. By perfectly following the FM wave's frequency, the PLL automatically creates a copy of the original signal.