Tools

Analog amplitude, frequency and phase modulation and demodulation with spectrum analysis

Amplitude Modulation (AM) and Demodulation

Theory :

Amplitude modulation (AM) is the process in which the amplitude of a carrier wave, denoted as \( c(t) = \cos(2\pi f_c t) \), is varied in proportion to the baseband signal. This modulation technique can be mathematically represented as:

\( s(t) = A_c \left[ 1 + K_a m(t) \right] \cos(2\pi f_c t) \)

or equivalently,

\( s(t) = A_c \cos(2\pi f_c t) + A_c K_a m(t) \cos(2\pi f_c t) \)

where:

  • \( K_a \) is the amplitude sensitivity of the modulator
  • \( s(t) \) is the modulated signal
  • \( A_c \) is the amplitude of the carrier signal
  • \( m(t) \) is the modulating (baseband) signal

Block Diagram for Amplitude Modulation

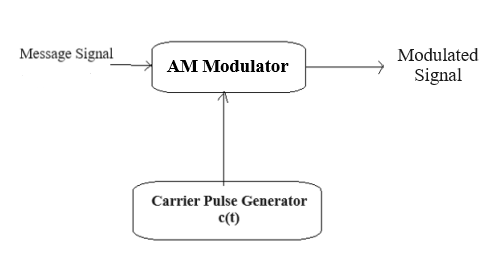
am_image2

Fig: Amplitude Modulation

Modulation Index (μ) in Amplitude Modulation

The modulation index \( \mu \) quantifies the extent to which the carrier amplitude varies in response to the message signal.

It is commonly defined as:
\( \mu = K_a A_m \), where:

  • \( A_m \) = peak amplitude of the message signal \( m(t) \)
  • \( A_c \) = carrier amplitude
  • \( K_a \) = amplitude sensitivity of the modulator


The value of \( \mu \) determines the modulation quality:

  • \( \mu < 1 \): Under-modulation
  • \( \mu = 1 \): 100% modulation (ideal)
  • \( \mu > 1 \): Over-modulation (leads to distortion)


Alternative definition:
Even if \( K_a \) and \( A_m \) are unknown, the modulation index can be calculated directly from the modulated waveform:

\( \mu = \frac{A_{\text{max}} - A_{\text{min}}}{A_{\text{max}} + A_{\text{min}}} \)
where:

  • \( A_{\text{max}} \) = maximum amplitude of the modulated signal
  • \( A_{\text{min}} \) = minimum amplitude of the modulated signal

Frequency Domain Description :

To understand the spectral characteristics of a AM wave, we analyze it in the frequency domain by applying the Fourier transform to its time-domain representation.

The AM signal is defined as:

\( s(t) = A_c \left[1 + k_a m(t)\right] \cos(\omega_c t) \)

Taking the Fourier transform of both sides, and applying frequency-shifting and delta function properties:

\( S(j\omega) = \pi A_c \left[ \delta(\omega - \omega_c) + \delta(\omega + \omega_c) \right] + \frac{1}{2} k_a A_c \left[ M(j(\omega - \omega_c)) + M(j(\omega + \omega_c)) \right] \)

This spectrum consists of two impulse functions weighted by the factor πAc, located at ±ωc, along with two replicas of the message spectrum that are shifted in frequency by ±ωc and scaled in amplitude by (1/2)kaAc.


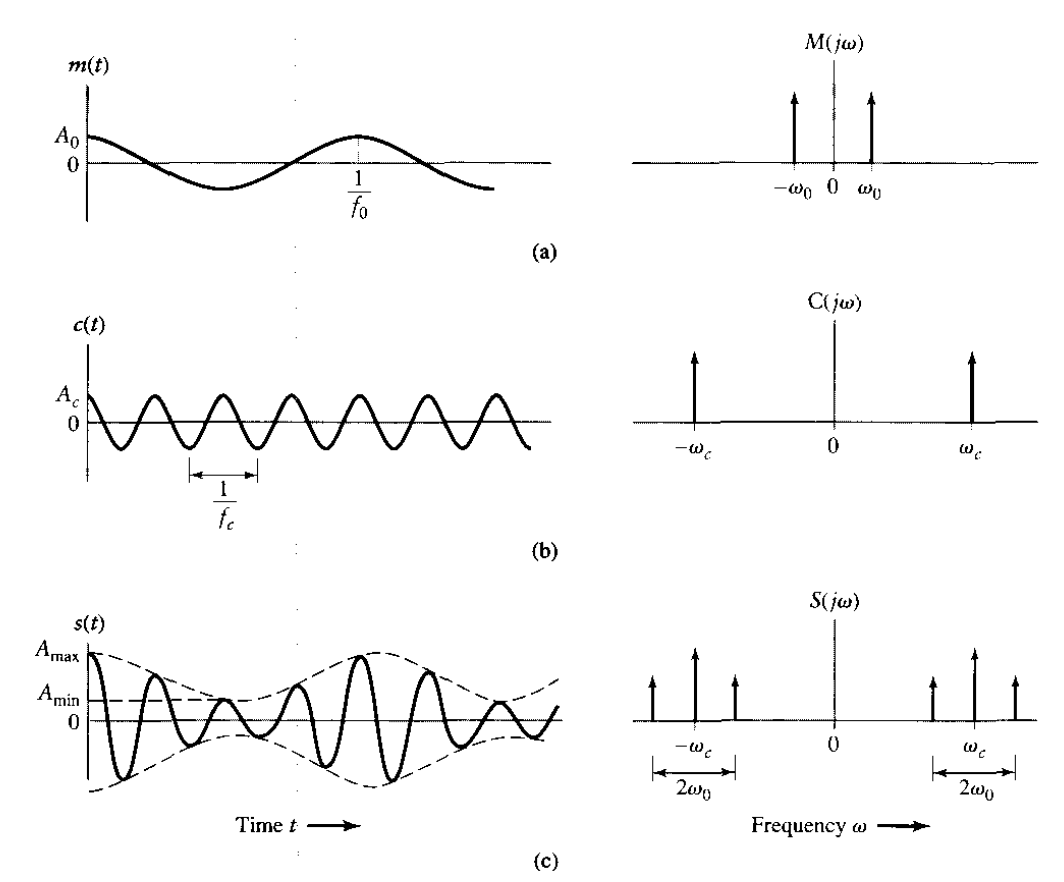
am_image1

Fig: Time-domain (on the left) and frequency-domain (on the right) characteristics of AM produced by a sinusoidal modulating wave. (a) Modulating wave. (b) Carrier wave. (c) AM wave.

Bandwidth

While the provided lab text displays the spectrum of an AM signal, it does not explicitly state the formula for calculating its required bandwidth. The bandwidth is defined as the difference between the highest and lowest frequencies present in the modulated signal's spectrum.

  • For a standard AM signal, the bandwidth is precisely twice the highest frequency component found in the modulating signal (also known as the message signal). The formula is:
    BW = 2 * fm
    Where fm is the maximum frequency of the message signal.

Block Diagram for Amplitude Demodulation

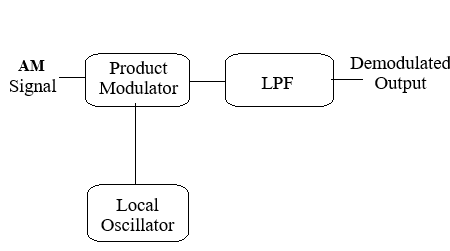
am_image2

Fig: Amplitude Demodulation


The block diagram illustrates the process of synchronous (coherent) demodulation, a method used to recover the original message signal from an Amplitude Modulated (AM) waveform.

  1. Modulated AM Signal Input:
    The input signal is given by:
    \( s(t) = A_c \left[1 + K_a m(t)\right] \cos(2\pi f_c t) \)
    Where:
    • \( A_c \): Carrier amplitude
    • \( f_c \): Carrier frequency
    • \( m(t) \): Message (modulating) signal
    • \( K_a \): Amplitude sensitivity constant

    2. The Product Modulator (Multiplier)

    The core of synchronous demodulation is multiplying the incoming AM signal \( s(t) \) with a locally generated carrier signal \( c(t) \). For ideal demodulation, this local carrier must be a perfect replica of the original transmitter's carrier:

    \( c(t) = \cos(2\pi f_c t) \)

    The multiplication yields the signal \( v(t) \):

    \( v(t) = s(t) \cdot c(t) = A_c [1 + K_a m(t)] \cos^2(2\pi f_c t) \)

    Using the trigonometric identity \( \cos^2(\theta) = \frac{1}{2} (1 + \cos(2\theta)) \), we can expand this equation:

    \( v(t) = \frac{A_c}{2} [1 + K_a m(t)] (1 + \cos(4\pi f_c t)) \)

    Distributing the terms gives:

    \( v(t) = \underbrace{\frac{A_c}{2} [1 + K_a m(t)]}_{\text{Low-Frequency Component}} + \underbrace{\frac{A_c}{2} [1 + K_a m(t)] \cos(4\pi f_c t)}_{\text{High-Frequency Component}} \)

    This multiplication effectively shifts the original message signal back to the baseband (centered around 0 Hz) and also creates a high-frequency component centered at twice the carrier frequency (\( 2f_c \)).


    The Low-Pass Filter (LPF)

    The output of the multiplier, \( v(t) \), is then passed through a Low-Pass Filter (LPF). The purpose of the LPF is to eliminate the high-frequency component at \( 2f_c \) while preserving the desired low-frequency (baseband) component.

    The filter is designed with a cutoff frequency that is:

    • Higher than the highest frequency in the message signal \( m(t) \).
    • Lower than the high-frequency component at \( 2f_c \).

    After filtering, the output signal, \( v_{LPF}(t) \), is:

    \( v_{LPF}(t) = \frac{A_c}{2} [1 + K_a m(t)] = \frac{A_c}{2} + \frac{A_c K_a}{2} m(t) \)

    This signal contains two parts:

    1. A DC offset: \( \frac{A_c}{2} \)
    2. A scaled version of the desired message signal: \( \frac{A_c K_a}{2} m(t) \)

    DC Blocking and Amplification

    To isolate the original message signal, the DC offset \( \frac{A_c}{2} \) must be removed. This is typically done using a simple DC-blocking capacitor or a level-shifting circuit. After removing the DC component, we are left with a scaled version of the message. An amplifier can then be used to scale the signal back to its original amplitude.