Objective:

This experiment covers the analysis of a frame using slope deflection method, computing the rotations, member end forces and moments and drawing the shear force and the bending moment diagrams of the deflected profile.

SOME FACTS:

(1) The slope deflection method is based on the application of equilibrium conditions at each joint or node in the structure. It considers both external loads and internal moments to determine displacements and rotations.

(2) The slope deflection method is based on the concept of slopes and rotations at the ends of structural members. It provides a geometric interpretation of how structural deformations and rotations affect the distribution of forces and moments within the structure.

Step-1: (a) Click on Bring button to display the structures . Step-1: (a) Click over the structure to choose for analysis .

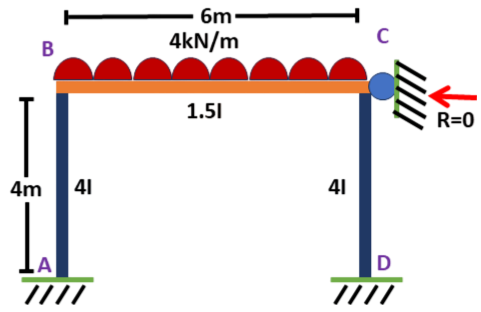Structural frame with UDL of 4kN/m along with the sway due to horizontal force of 12kN Start Analysis

Step-1 Calculation of Fixed End Moments

For Span BC

M^F_BC = [ W x L² ] / 12

M^F_BC = [     x 6² ] / 12 =

Solve

For Span CB

M^F_CB = -[ W x L² / 12 ]

M^F_CB = -[ 4 x     ] / 12 =

Solve

Note:
M^f_AB = M^f_BA = M^f_CD = M^f_DC = 0
(Since there is no load in column AB and CD )

Moment acting in anti-clockwise derection ↻ = +ve
Moment acting in clockwise derection ↺ = -ve

Step-2 Slope Deflection Equation

For column AB and CD

1. M_AB = M^f_AB + [(2E(4I) / L) (2Θ_A + Θ_B)]

1. M_AB =            + [(2E(4I) /     ) (0 + Θ_B)]

-------(1)

Solve

Similarly

-------(2)

2. M_BA = M^f_BA + [(2E(4I) / L) (2Θ_B + Θ_A)]

3. M_CD = M^f_CD + [(2E(4I) / L) (2Θ_C + Θ_D)]

-------(3)

4. M_DC = M^f_DC + [(2E(4I) / L) (2Θ_D + Θ_C)]

-------(4)

1: There is sway mechanism in the beam towards right
2: Θ_A & Θ_B = Slope at pt. A & B
3: δ = Sway towards right (+ve)

Slope Deflection Equation

For Beam BC

M_BC = M^f_BC + [2E(1.5I) / L] (2Θ_B + Θ_C)

1. M_BC =     + [2E(1.5I) /     (2Θ_B + Θ_C)]

Solve

-------(5)

Similarly

-------(6)

Joint Equiliberium Equations

At Joint B: M_BA and M_BC = 0

i.e 4EIΘ_B + 12 + EIΘ_B + 0.5EIΘ_C = 0

5EIΘ_B + 0.5EIΘ_C = -12 ---------(7)

Similarly At Joint C: M_CB and M_CD = 0

i.e (-12 + 0.5EIΘ_B + EIΘ_C) + (4EIΘ_C) = 0

0.5EIΘ_B + 5EIΘ_C = 12 ---------(8)

Step-3 Calculations for Final Moments

The Kinematic indeterminacy of the frame is 2 so that we have unknowns (Θ_B, Θ_C).

also, after solving the equilebrium equations (7) and (8) we get,

EIΘ_B = -2.667
EIΘ_C = 2.667

Moments

Applying values of EIΘ_Band EIΘ_Cin eqⁿ. (1) and (2)

M_AB = 2 x EIΘ_B---> 2 x       =

Solve

Similarly: M_BA = 4 x EIΘ_B

Also, from equation (3) and (4)

Applying values of EIΘ_C in eqⁿ. (5) & (6)

M_CD = 4 x EIΘ_C ---> 4 x       =

Solve

Similarly: M_DC = 2 x EIΘ_C =

Step-4 Calculations for Horizontal and Vertical Reactions

Now We have Moments M_ABM_BAM_CD and M_DC Now lets find:

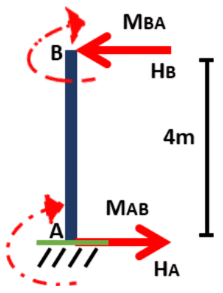
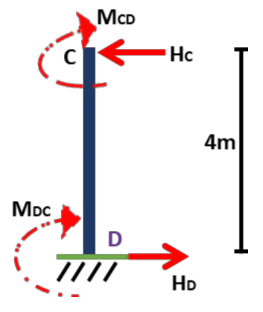
1. Horizontal reactions about B ↻ = -ve, ↺ = +ve

we have: 4H_A - M_AB - M_BA = 0

4H_A -       +         =

Solve

Now we consider ΣH = 0

    + H_B =

Solve

Similarly horizontal reaction about D

4H_D - M_CD - M_DC = 0

and again consider ΣH = 0

H_C + H_D = 0 then

2. Vertical reactions about B [↻ = +ve, ↺ = -ve ]

Since Beam BC is having symetrical loading then,

V_B = -(W x l) / 2 ---> -     x     / 2 =

Solve

Similarly V_C = (W x l) / 2 --->

Moment Diagrams

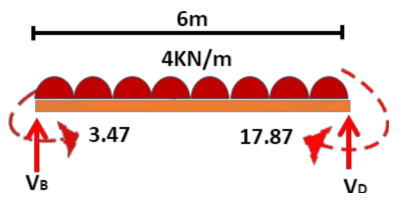
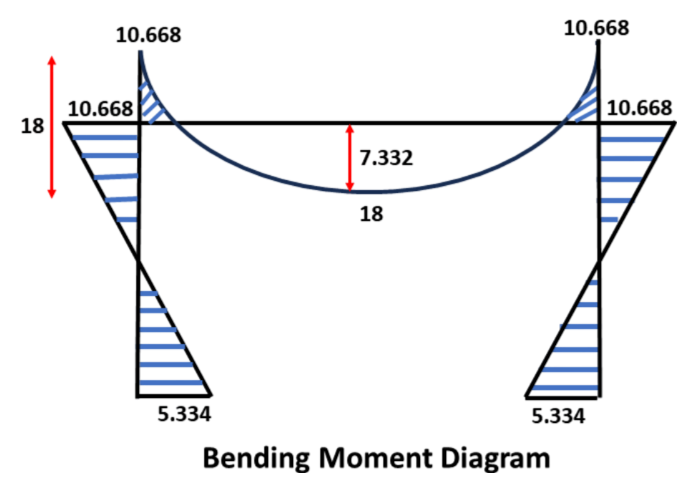
Shear Force Values

Moment_AB (M_AB) = -5.334 kNm

Moment_BA (M_BA) = -10.668 kNm

Moment_BC (M_BC) = 10.668 kNm

Moment_CB (M_CB) = -10.668 kNm

Moment_CD (M_CD) = 10.668 kNm

Moment_DC (M_DC) = 5.334 kNm