Objective:

To analyse a beam structure using slope deflection method

SOME FACTS:

(1) Historical Significance: The slope-deflection method was developed by Hardy Cross, an American engineer, in the 1930s. It was one of the earliest methods for analyzing indeterminate structures, preceding the development of the matrix stiffness method and the finite element method.

(2) Kinematic Compatibility: The method is based on the assumption of kinematic compatibility, meaning that the rotations at the joints or supports of a structure must be compatible with each other. This is a fundamental concept in the method.

Step-1: (a) Click on Bring button to display the structures . Step-1: (a) Click over the structure to choose for analysis .

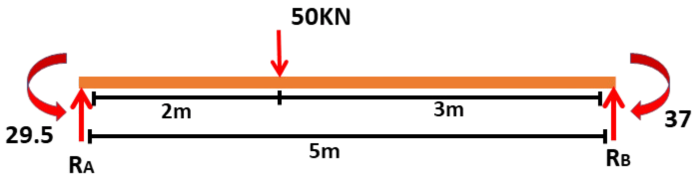
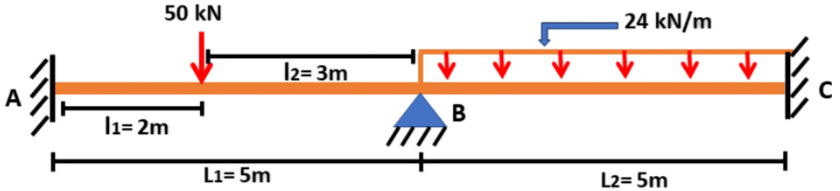Beam with a point load of 50kN applied at distance of 2m from point A and a UDL over the span of 5m

Note: Please draw the structure on a paper and note down the calculations

Start

Step- 1 Calculation of Fixed End Moments

For Span AB

M^F_AB = [ P x l₁ x (l₂)² ] / L ²

M^F_AB = [          x 2 x (3)² ] / 5 ² =

Calc.

For Span BA

M^F_BA = [ -P x (l₁²) x l₂ ] / L²

M^F_BA = [ -50 x           x 3 ] / 5 ² =

Solve

For Span BC

M^F_BC = [ W x L₁² / 12 ]

M^F_BC = [ 24 x           ] / 12 =

Solve

For Span CB

M^F_CB = -[ W x L₂² / 12 ]

M^F_CB = -[          x 5² ] / 12 =

Solve

Have you noted Down the calculations?

CONDITIONS:
Moments in anticlockwise ↺ = +ve

Yes

Step-2 Slope Deflection Equation

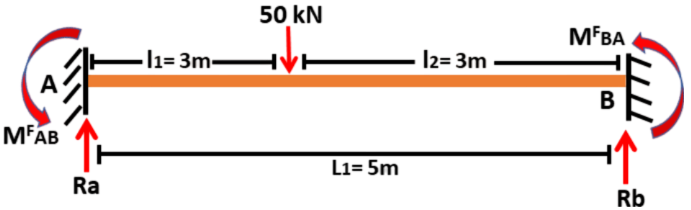
For Span AB

M_AB = M^F_AB + (2EI / L) (2Θ_A+ Θ_B)

1. M_AB =     + (2EI /     ) (      + Θ_B)

Solve

------------(1)

Similarly

2.

M_BA = M^F_BA + (2EI / L) (2Θ_B+ Θ_A)

------------(2)

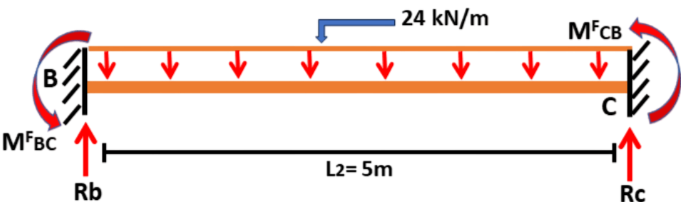
3.

M_BC = M^F_BC + (2EI / L) (2Θ_B + Θ_C)

------------(3)

4.

M_CB = M^F_CB + (2EI / L) (2Θ_C + Θ_B)

------------(4)

CONDITIONS:
1- No of supports at which slope (Θ) occerse is 1.
2- Slope Θ_B is present at point B (Hinge Support).
3- No. of unknowns = 1.
4- No. of equilibrium equations = 1.

Step-3 Final Moments

Equiliberium Equation

In This problem there is only one unknown ie. EIΘ_B

M_BA + M_BC = 0 :

-24 + 0.8EIΘ_B + 50 + 0.8EIΘ_B = 0

EIΘ_B = -16.25

Calculation for final moments

Substituting value of EIΘ_B in Equation 1, 2, 3 and 4

M_AB= 36 + 0.4EIΘ_B = 36 + 0.4 x            =

Similarly

M_BA= -24 + 0.8EIΘ_B = -24 + 0.8 x (-16.25) = -37 kNm

M_BC= 50 + 0.8EIΘ_B = 50 + 0.8 x (-16.24) = 37 kNm

M_CB= -50 + 0.4EIΘ_B= -50 + 0.4 x (-16.24)= -56.5 kNm

Solve

Step-2 Calculations for member end shear force for AB and BC

Taking Moments about B

-5R_A + (50 x 3) + M_A - M_B = 0

-5R_A + 150 +           -           = 0

R_A=

Solve

Reaction at left part of B

ΣV = 0 then, R_B1 + R_A - 50 = 0

         + R_B1 - 50 = 0

R_B1=

Solve

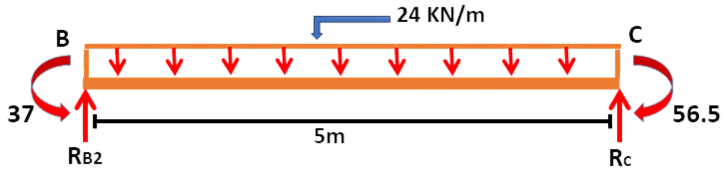
Taking Moments about C

-5R_B2 + UDL (5 x 5/2) + M_BC - M_CB = 0

-5R_B2+ (           x 12.5) - 19.5 = 0

R_B2=

Solve

Reaction at right part of B

ΣV = 0 then, -R_B2 - R_C + 24 X 5 = 0

-           - R_C + 24 X 5 = 0

R_C=

Reaction at Pt. B (R_B)
= R_B1 + R_B2 → 21.5 + 56.1 = -77.6 kN

Solve

CONDITIONS:
1- Moments in clockwise direction ↻ is +ve
2- Moments in anti-clockwise direction ↺ is -ve
3- Rule: Σ of all vertical forces = 0 (ΣV = 0)

Shear Force Diagram

Shear Force at A = 28.5 kN

Shear Force at left of W1 = 28.5 kN

Shear Force at right of W1 = 28.5 + 50 = 21.5 kN

Shear Force at left of B = 21.5 kN

Shear Force at right of B = 21.5 - 77 = 56.1 kN

Shear Force at left of C = 56.1 + 24 x 5 = 63.9 kN

Shear Force at C = 63.9 - 63.9 = 0 kN

Plot SFD

Bending Moment Diagram from tension side

We consider every space as seperate simply supported beam