Passband Phase Shift Keying (PSK)

Theory:

PSK is a digital modulation scheme analogous to phase modulation. Binary Phase Shift Keying (BPSK) is the simplest form of PSK. In BPSK, two output phases are possible for a single carrier frequency, representing logic '1' and logic '0'. As the input digital binary signal changes state, the phase of the output carrier shifts by 180 degrees. In a PSK modulator, the carrier input signal is multiplied by the digital data. Each change in the input logic condition will consequently change the output phase. For PSK, the output rate of change equals the input bit rate, and the widest output bandwidth occurs when the input binary data is an alternating '1/0' sequence. The fundamental frequency of an alternating '1/0' bit sequence is equal to one-half of the bit rate.

Baseband PSK:

Baseband PSK refers to the representation of the digital data (symbols) before it modulates a high-frequency carrier. In BPSK, for instance, binary '0' can be mapped to a voltage level of '-1' and binary '1' to '+1'. These baseband signals are then used to control the phase of the carrier in the passband modulation process. This baseband signal typically has spectral components centered around zero frequency.

Passband PSK:

**Passband PSK** refers to the modulated signal that occupies a specific frequency band around a carrier frequency (f_c) for transmission over a physical medium. In **passband BPSK modulation**, the transmitted signal is created by shifting the phase of a high-frequency carrier wave based on the binary data. For example, if the carrier is A_ccos(2Пf_ct), a binary '1' can be represented by a 0-degree phase shift (A_ccos(2Пf_ct)), and a binary '0' by a 180-degree phase shift (A_ccos(2Пf_ct + П) = -A_ccos(2Пf_ct)). The modulated signal, existing in the passband, is then suitable for transmission over channels like radio or optical fiber.

Passband PSK Transmitter:

In BPSK, binary ‘1’ is represented by the actual carrier phase, and binary ‘0’ by a 180-degree phase shift of the carrier. This results in a passband signal.

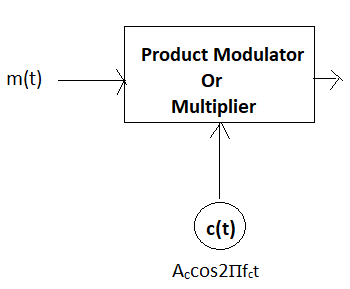
For a carrier A_ccos(2Пf_ct), the passband signals are:
1 => S₁(t) = A_ccos(2Пf_ct)
0 => S₂(t) = A_ccos(2Пf_ct + 180°) = -A_ccos(2Пf_ct)

Here, the baseband signaling scheme for the data is often NRZ (Non-Return-to-Zero), where:
1 = +ve voltage level (e.g., +1V)
0 = -ve voltage level (e.g., -1V)
This baseband signal then modulates the phase of the carrier to produce the final passband PSK signal.

Passband PSK Receiver (Coherent Demodulation Example):

For the demodulation of passband BPSK, a coherent detector is typically used, which requires a local carrier signal synchronized in phase and frequency with the transmitted carrier. This allows for the down-conversion of the passband signal back to baseband for detection.

Assuming a coherent receiver multiplies the received passband signal by the synchronized local carrier A_ccos(2Пf_ct) and integrates over a bit period T_b:
If binary '1' was sent (passband signal S₁(t)):
∫₀^T_b (A_ccos(2Пf_ct) ⋅ A_ccos(2Пf_ct)) dt ≈ (A_c)²/2 ⋅ T_b (after filtering high frequency terms)
This value would be greater than a certain threshold V_th.
If binary '0' was sent (passband signal S₂(t)):
∫₀^T_b (-A_ccos(2Пf_ct) ⋅ A_ccos(2Пf_ct)) dt ≈ -(A_c)²/2 ⋅ T_b (after filtering high frequency terms)
This value would be less than the threshold V_th.

Constellation Diagram of Passbnad BPSK

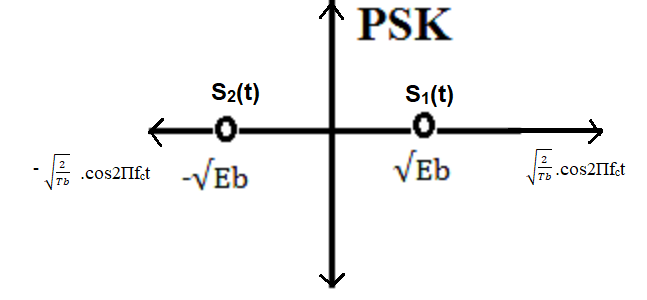
Figure: Constellation Diagram of BPSK

So, the energy of symbol S₁ is (√(E_b))² = E_b
And the energy of symbol S₂ is (-√(E_b))² = E_b

The Euclidean distance between the signaling points, d₁₂ = |√(E_b) - (-√(E_b))| = 2√(E_b)
This distance is crucial for determining the probability of error in the presence of noise.
High-order PSK (e.g., QPSK, 8-PSK, 16-PSK) can transmit more bits per symbol but is more sensitive to noise (requires higher SNR for the same error rate). Low-order PSK (e.g., BPSK, QPSK) is less susceptible to noise.
PSK modulation can be visualized using a constellation diagram, where each point represents a symbol. In the presence of noise, points may be away from their original positions, making them harder to distinguish and increasing the probability of error.

Passband BPSK Under different noise configurations

Passband PSK Modulation with AWGN
In passband PSK modulation, digital data is represented by varying the phase of the carrier signal. Binary PSK (BPSK) is a common form of PSK modulation where the carrier phase is shifted by 180 degrees for different binary symbols, creating a signal in the passband.

Mathematically, the BPSK-modulated passband signal x(t) can be represented as:
x(t) = A_ccos(2Пf_ct), { for binary symbol 1}
x(t) = A_ccos(2Пf_ct + П) = -A_ccos(2Пf_ct), { for binary symbol 0}

Where:
f_c is the carrier frequency.
A_c is the carrier amplitude.

In the presence of Additive White Gaussian Noise (AWGN), the received passband signal y(t) becomes:
y(t) = x(t) + n(t)
Where:
x(t) is the PSK-modulated signal in the passband.
n(t) is the AWGN, characterized by a flat power spectral density (N₀/2) across all frequencies, affecting the passband signal.

The AWGN introduces random voltage fluctuations that are added to the passband signal, affecting both its amplitude and phase components in the receiver's observation space. Since PSK relies on phase differences for symbol differentiation, the noise can cause the received phase to deviate from the ideal transmitted phase, leading to errors in demodulation if the deviation is large enough. The SNR (signal-to-noise ratio) at the receiver plays a crucial role in determining the quality of demodulation, with higher SNR leading to lower error rates.

Passband PSK Modulation with Rayleigh Fading:
Rayleigh fading introduces random amplitude and phase variations to the received passband signal due to multipath propagation, typically in urban environments or non-line-of-sight scenarios. In the case of PSK modulation, the mathematical representation of the received passband signal y(t) under Rayleigh fading is:
y(t) = h(t) ⋅ x(t) + n(t)
Where:
h(t) is the complex fading coefficient, which is a complex Gaussian random variable with a Rayleigh distributed magnitude and uniformly distributed phase. It models the attenuation and phase shift introduced by the fading channel on the passband signal.
x(t) is the PSK-modulated passband signal.
n(t) is the AWGN.

The fading coefficient h(t) introduces random variations in both the amplitude and phase of the received passband signal components. These variations can significantly distort the phase of the PSK signal, making accurate phase detection challenging. This leads to a higher bit error rate (BER) compared to AWGN channels, especially in deep fades where the signal strength drops significantly. Techniques like diversity and channel coding are often employed to mitigate the effects of Rayleigh fading on PSK passband signals.

In summary, PSK modulation performance is highly dependent on the noise environment. AWGN introduces uniform noise, affecting the decision regions on the constellation. Rayleigh fading introduces random amplitude and phase distortions, which can be more detrimental to PSK's phase-dependent detection. The reliability of PSK demodulation depends on the SNR for AWGN and the characteristics and mitigation strategies for the fading channel.

PSK modulation offers advantages in scenarios with favorable SNR but can be sensitive to phase changes in noisy or interference-prone, or fading environments. Its performance depends on factors like modulation order, carrier synchronization accuracy, and the presence of various distortions affecting the passband signal. Employing techniques such as FEC and adaptive modulation can help optimize PSK modulation's performance in diverse scenarios.