Passband Frequency Shift Keying (FSK)

Theory:

Frequency Shift Keying (FSK) is a digital modulation technique where digital information is represented by changes in the frequency of a carrier wave. Instead of varying amplitude (as in ASK) or phase (as in PSK), FSK encodes data by shifting the carrier frequency among a set of discrete, predefined frequencies. This makes FSK relatively robust against amplitude variations and noise compared to ASK.

The simplest form is Binary FSK (BFSK), which uses two distinct frequencies to transmit binary '0's and '1's. When a binary '1' is to be transmitted, the carrier is set to a "mark" frequency (f₁). When a binary '0' is to be transmitted, the carrier is set to a "space" frequency (f₂). These two frequencies are typically chosen such that they are orthogonal over the bit duration, which simplifies demodulation.

Passband FSK signals are designed to occupy a specific frequency band around these carrier frequencies, making them suitable for transmission over analog communication channels like wireless links or optical fibers.

Baseband vs. Passband FSK:

Baseband Signaling: In baseband transmission, digital data is represented directly by electrical pulses (e.g., NRZ, RZ) transmitted over a wired medium. No carrier modulation is involved, and the signal spectrum extends from DC (0 Hz). While conceptually one could "map" bits to certain baseband voltage levels, there isn't a direct "baseband FSK" in the same sense as passband FSK because FSK inherently involves modulating a carrier frequency.

Passband FSK: In passband FSK, the digital information modulates the frequency of a high-frequency sinusoidal carrier. The resulting modulated signal occupies a specific band of frequencies centered around the chosen carrier frequencies (f₁ and f₂). This allows the signal to be transmitted efficiently over analog channels that are designed for specific frequency ranges, without occupying frequencies down to DC. For example, in wireless transmission, two different radio frequencies are used to represent '0' and '1'.

Passband FSK Transmitter:

A Passband FSK transmitter typically uses a Voltage-Controlled Oscillator (VCO) or a frequency synthesizer. The input binary data stream (often represented by a bipolar baseband signal, e.g., '1' as +V and '0' as -V) modulates the control voltage of the VCO.

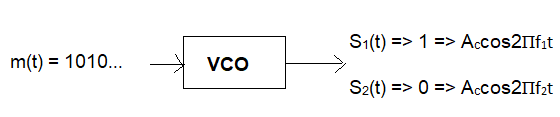
When the input is for binary '1', the VCO generates a carrier signal at frequency f₁. When the input is for binary '0', the VCO generates a carrier signal at frequency f₂. The amplitude of the carrier remains constant.

The mathematical representation of a binary FSK signal for a bit duration T_b is:
s₁(t) = A_c cos(2πf₁t + φ)   for binary '1'
s₂(t) = A_c cos(2πf₂t + φ)   for binary '0'
where A_c is the constant carrier amplitude, f₁ and f₂ are the two distinct frequencies, and φ is the initial phase. For coherent FSK, the phase φ is maintained across bit transitions, while for non-coherent FSK, it can be discontinuous.

A common method for generating FSK is to switch between two different oscillators or to use a single oscillator whose frequency is controlled by the data signal.

VCO Principle:

A Voltage Controlled Oscillator (VCO) generates an output frequency that is proportional to its input voltage. In the context of FSK, the binary data stream (after conversion to appropriate voltage levels) is fed into the VCO as the control voltage.
For a simple LC tank circuit, the resonant frequency is f = 1 / (2π√(LC)). If a varactor diode (whose capacitance C' changes with reverse bias voltage) is used in the tank circuit:
f = 1 / (2π√[L(C + C')]).

Transmission of binary ‘1’:

If the binary '1' is represented by a higher control voltage (e.g., a positive voltage from an NRZ encoder), and this voltage reverse-biases a varactor diode more strongly. A higher reverse bias voltage increases the width of the depletion layer in the varactor diode, which decreases its capacitance (C').
Since f = 1 / (2π√[L(C + C')]), a decrease in C' leads to an increase in the oscillation frequency. This higher frequency corresponds to f₁ (mark frequency).

Transmission of binary ‘0’:

If the binary '0' is represented by a lower control voltage (e.g., zero or a negative voltage from an NRZ encoder), and this voltage reduces the reverse bias (or even forward-biases) the varactor diode. A reduced reverse bias (or forward bias) decreases the width of the depletion layer, which increases its capacitance (C').
An increase in C' leads to a decrease in the oscillation frequency. This lower frequency corresponds to f₂ (space frequency).
Thus, typically, f₁ > f₂.

Passband FSK Receiver (Coherent Demodulation Example):

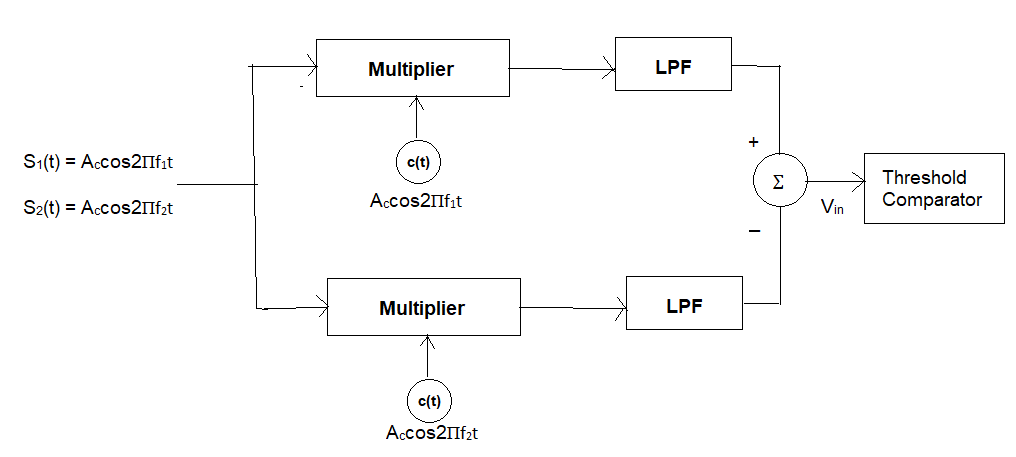
Coherent FSK demodulation, similar to coherent ASK, requires synchronization of local oscillators with the incoming carrier frequencies. A common method uses two correlators or matched filters, each tuned to one of the possible carrier frequencies (f₁ and f₂).

The received FSK signal is fed into two branches.
Upper Branch (for f₁ detection): The received signal is multiplied by a locally generated carrier A_ccos(2πf₁t) (synchronized in frequency and phase) and integrated over the bit duration T_b.
If s₁(t) = A_ccos(2πf₁t) was transmitted, the output of the integrator will be proportional to the energy of s₁(t), i.e., (A_c²/2)T_b.
If s₂(t) = A_ccos(2πf₂t) was transmitted, and f₁ and f₂ are orthogonal, the output of this integrator will be ideally zero.

Lower Branch (for f₂ detection): Similarly, the received signal is multiplied by A_ccos(2πf₂t) and integrated over T_b.
If s₂(t) was transmitted, the output will be (A_c²/2)T_b.
If s₁(t) was transmitted, the output will be ideally zero.

The outputs of the two integrators are then fed into a comparator. If the output from the f₁ branch is significantly higher than the f₂ branch, a '1' is detected. Conversely, if the f₂ branch output is higher, a '0' is detected. This is often implemented with a subtractor followed by a decision device.
This type of receiver is known as a Coherent BFSK receiver. Non-coherent FSK receivers, which do not require phase synchronization, are also widely used due to their simpler design, though they typically have slightly worse performance in terms of error rate for a given SNR.

Constellation Diagram of Passband FSK

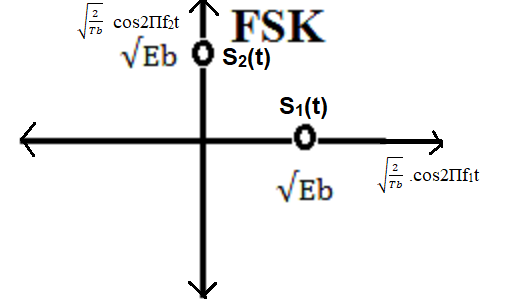
Figure: Constellation Diagram of Orthogonal Binary Passband FSK

The two signal points are located on orthogonal axes at a distance of √E_b from the origin.
The Euclidean distance between the two signaling points, d₁₀ = √[( √E_b - 0 )² + ( 0 - √E_b )²] = √[E_b + E_b] = √(2E_b).
This distance is crucial for determining the error performance of the system in noise.
High-order FSK (M-FSK) uses M different frequencies to represent log₂M bits per symbol. This would result in M points in an M-dimensional constellation diagram, typically located at the corners of a hypercube, each at a distance of √E_s (where E_s is the symbol energy) from the origin.

Passband FSK Under Different Noise and Channel Configurations

The performance of Passband FSK is affected by noise and channel characteristics.

Passband FSK Modulation with Additive White Gaussian Noise (AWGN):

When a passband FSK signal is transmitted through a channel impaired by AWGN, the noise affects the received signal in the frequency domain.
The received signal y(t) is given by:
y(t) = s(t) + n(t)
Where:
s(t) is the FSK-modulated signal (either s₁(t) or s₂(t)).
n(t) is the AWGN.

In the receiver, the AWGN introduces random voltage fluctuations across the signal's bandwidth. For coherent FSK, the noise at the output of the correlators can cause the decision variable to be ambiguous, leading to errors. However, because FSK encodes information in frequency changes, it is generally more robust to amplitude distortions from AWGN than ASK. The probability of error for FSK depends on the Euclidean distance between the signal points in the constellation diagram and the noise power, quantified by the Signal-to-Noise Ratio (SNR).

Passband FSK Modulation with Rayleigh Fading:
Rayleigh fading, common in wireless environments without a direct line-of-sight path, causes random and rapid fluctuations in the amplitude and phase of the received signal due to multipath propagation.
The received signal y(t) in the presence of Rayleigh fading is:
y(t) = h(t) * s(t) + n(t)
Where:
h(t) is the complex fading coefficient, whose magnitude |h(t)| follows a Rayleigh distribution.
s(t) is the FSK-modulated signal.
n(t) is the AWGN.

While FSK is more resilient to amplitude variations than ASK, significant fading can still degrade its performance. If deep fades occur, the amplitude of both f₁ and f₂ components can drop simultaneously, making detection difficult. Furthermore, frequency-selective fading (where different frequencies within the signal bandwidth fade independently) can distort the spectral shape of the FSK signal, potentially leading to inter-symbol interference if the symbol rate is high. Non-coherent FSK is often preferred in fading channels due to its simpler implementation and less stringent synchronization requirements, even if it has a slightly higher error rate in AWGN. Diversity techniques and channel coding are crucial for reliable FSK communication in fading environments.

In conclusion, Passband FSK is a valuable modulation technique, particularly where simplicity and robustness against amplitude disturbances are priorities. Its performance is strong in noisy environments (relative to ASK) but its spectral efficiency is lower than phase-based schemes. It is widely used in applications ranging from simple telemetry to some forms of radio data transmission.