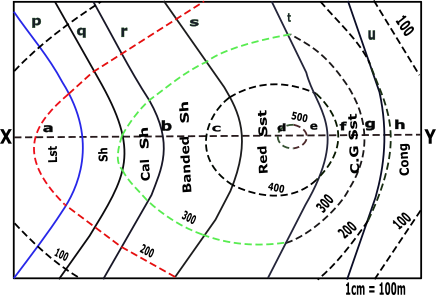
CONTOUR MAP
Objective:
- Draw a geological cross-section along XY.
- Find the vertical thickness of beds.
- A horizontal tunnel is proposed at an altitude of 100m.
Pre-requisites:
Topographic map
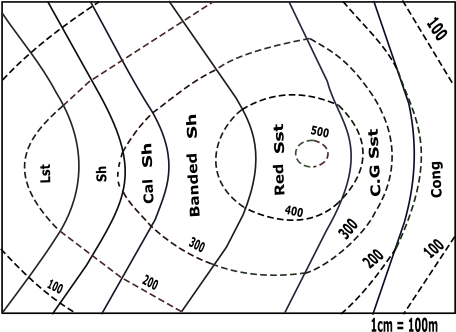
Description Strata: In geology and related fields, a stratum (plural: strata) is a layer of sedimentary rock or soil, or igneous rock that were formed at the Earth's surface, with internally consistent characteristics that distinguish it from other layers.
Vertical thickness:Thickness of rock body measured vertically is called vertical thickness.
Identify the line about which the profiles are to be drawn.
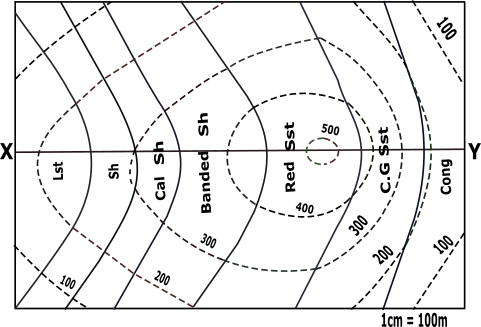

Line to be considered for profiles to be drawn:
Mark all the points of XY line that is obtained by the intersection of the dotted line with this XY of the contour map.
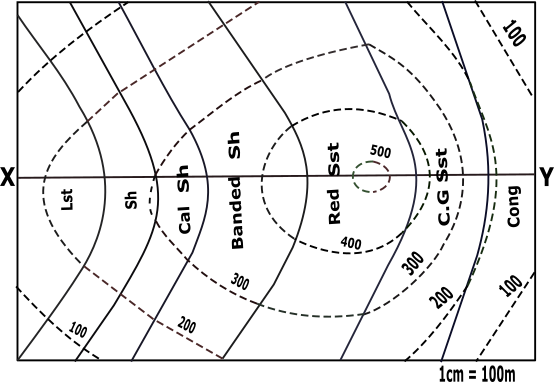
| Points | X-Co | Y-Co |
|---|---|---|
| a | x1 | 200 |
| b | x2 | 300 |
| c | x3 | 400 |
| d | x4 | 500 |
| e | x5 | 500 |
| f | x6 | 400 |
| g | x7 | 300 |
| h | x8 | 200 |
Identify X-axis and Y-axis taking X as origin and define scale.
Plot the points taking its distance from X as x coordinate and the index values of the corresponding line as y coordinate along with the points Y’ (1535,0) on the graph.
| Points | X-Co | Y-Co |
|---|---|---|
| a | 90 | 200 |
| b | 400 | 300 |
| c | 710 | 400 |
| d | 990 | 500 |
| e | 1100 | 500 |
| f | 1210 | 400 |
| g | 1330 | 300 |
| h | 1420 | 200 |
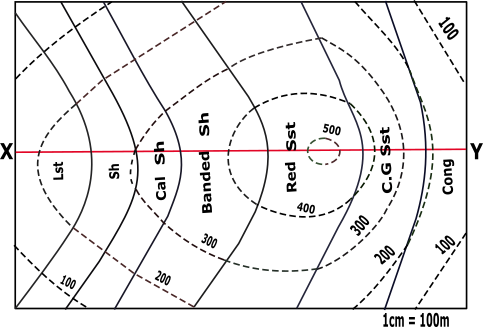
Mark all the points of XY line that is obtained by the intersection of the solid line with this XY of the contour map.

| Points | X-Co | Y-Co |
|---|---|---|
| p | x1 | y1 |
| q | x2 | y2 |
| r | x3 | y3 |
| s | x4 | y4 |
| t | x5 | y5 |
| u | x6 | y6 |
Name the points as p,q,r … respectively taking its distance from X as x-coordinate.
| Points | X-Co | Y-Co |
|---|---|---|
| p | x1 | y1 |
| q | x2 | y2 |
| r | x3 | y3 |
| s | x4 | y4 |
| t | x5 | y5 |
| u | x6 | y6 |
To Calculate the index value of the solid line.
➤Search for the first dotted line on both the sides of the solid line.Let their index values be M and N.
➤Let α be the x-coordinate for dotted line with index value M from Table 1
➤Let β be the x-coordinate for dotted line with index value N from Table 1
➤Let ¥ be the x-coordinate for selected solid line from Table 2.
➤The index value of the solid line is given by
➤For α>β:Index= (N*(α- ¥)+M*(¥- β))/( α- β)
➤For α<β:Index=(N*(¥- α )+M*( β-¥))/( β- α)

Calculate the index value of all solid lines.
Hint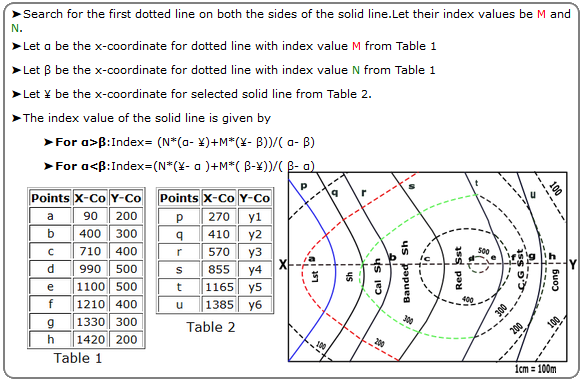
| Points | X-Co | Y-Co |
|---|---|---|
| a | 90 | 200 |
| b | 400 | 300 |
| c | 710 | 400 |
| d | 990 | 500 |
| e | 1100 | 500 |
| f | 1210 | 400 |
| g | 1330 | 300 |
| h | 1420 | 200 |
| Table 2 | ||
|---|---|---|
| Points | X-Co | Y-Co |
| p | 270 | y1 |
| q | 410 | y2 |
| r | 570 | y3 |
| s | 855 | y4 |
| t | 1165 | y5 |
| u | 1385 | y6 |
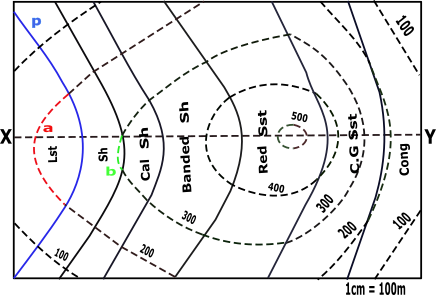

➤For the solid line p:
Plot the above points (p to u) with the plotted points (a to h) along with the points Y’ (1535,0) on the graph.
| Points | X-Co | Y-Co |
|---|---|---|
| p | 270 | 258 |
| q | 410 | 303 |
| r | 570 | 355 |
| s | 855 | 452 |
| t | 1165 | 441 |
| u | 1385 | 239 |
Join all the plotted points on the graph. And extrapolate it between the bounds.
A horizontal tunnel is proposed at an altitude of 100m from the x axis parallel to it, between the bounds.
Calculation for Angle of dip.
➤Search for the points of intersection between the solid line and the dotted line on the contour map.
T1=100 T2=200

T2>T1
θ=45º
From the points (p,q,r,s,t,u) draw a line at an angle θ with horizontal in anticlockwise direction and its point of intersection on x-axis be (p’,q’,r’,s’,t’,u’) respectively.
➤p-p’☚
➤q-q’☚
➤r-r’☚
➤s-s’☚
➤t-t’☚
➤u-u’☚
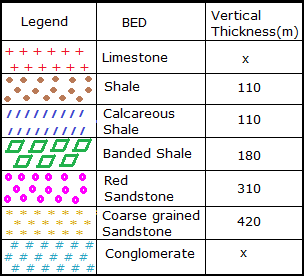
Location of types of stones on the contour.
➤Lst☚
➤Sh☚
➤CalSh☚
➤BandSh☚
➤RedSst☚
➤CGSst☚
➤Cong☚
Find out the vertical thickness of beds.
| Region | Vertical Thickness |
|---|---|
| Lst | x |
Profile View Graph
**Hover over Scale, Direction, Legend and Points to see description of graph**
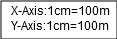



Both ends of the pipe must be trimmed to ensure parallel faces.
