CLICK OVER THE STATES TO CHOOSE THEM AS MINIMUM ENERGY STATES
YOU CAN CHOOSE AT MOST TWO STATES AS MINIMUM
MAKE SURE THEY ARE SEPARATED BY MORE THAN ONE HAMMING DISTANCE

Hamming distance is often calulated with two text or numeric input of same size. The number of place in which one value is differing from other is known as hamming distance or in better words "How many minimum places need to change in one input to get second input.".
The most common example of hamming distance is that it is used in computer networking. The number of bits get corrupted while transmitting via a network is calculated by hamming distance.
1. We traverse from the first to last bit/word/number of both the inputs. Initially, the hamming distance is set to zero.
2. We begin to traverse both the inputs from the beginning and check one by one the bit/word/number of both the inputs. While iteration we check whether the input bit/word/number of both the places are same or not.
3. If the bits/words/numbers are same, we go to the next bit/word/number of both the inputs.
4. If the bits/words/numbers are having different values then the hamming distance is increased by one.
5. The final hamming distance value is the answer.
Hamming Distance = 2 (2nd and 3rd position are different).
Hamming Distance = 2 (2nd and 3rd position are different).
Hamming Distance = 3 (4th,9th and 11th position are different).
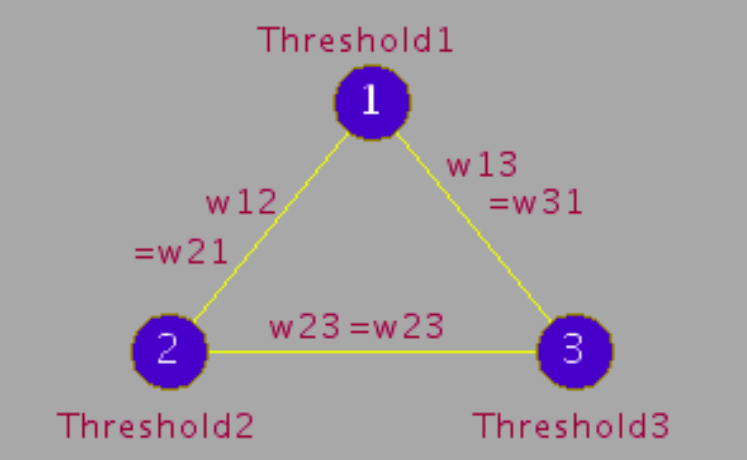
THE FOLLOWING ACTIVATION DYNAMICS EQUATIONS MUST BE SATISFIED:
ADJUST THE WEIGHTS AND THRESHOLD FOR NEW STD
W12 = W21 Value:
W23 = W32 Value:
W31 = W13 Value:
Threshold 1 Value:
Threshold 2 Value:
Threshold 3 Value:
0 0 0
0 0 1
0 1 0
1 0 0
0 1 1
1 0 1
1 1 0
1 1 1