Objective
To determine the convective heat transfer coefficient and the rate of heat transfer by forced convection for flow of air inside a horizontal pipe.
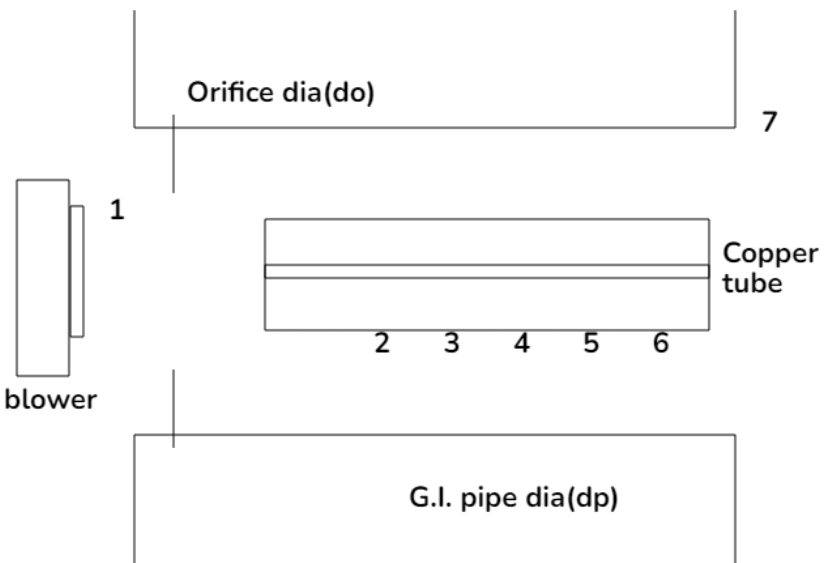
Dp - 40mm
Do - 20mm
specimen dimension - 23x300 mm
Set voltage
Temperature Gradient
$$Properties \space of \space air \space at \space T_m$$
$$T_m = \frac{(T_s + T_a)}{2} K$$
$$T_s = \frac{(T_2+T_3+T_4+T_5+T_6)}{5} K$$
$$T_a = 303 K$$
$$Mass \space density \space of \space air = 1.12 kg/m^3$$
$$h_a = \frac{\rho m. hm}{\rho a}m$$
$$\rho m(mercury) = 13600 kg/m^3$$
$$Manometer \space Reading \space hm = 25mm$$
$$h_a = $$
$$m$$
$$V_o = \frac{C_d. (2.g.h_a)^{1/2}}{(1-(d_0/d_p)^4)^{1/2}} m/s$$
$$C_d= 0.6$$
$$V_o = $$
$$m/s$$
$$V_a = $$
$$m/s$$
$$R_e = \frac{V_a.d_s}{\gamma}$$
$$\gamma = 1.696*10^{-5}$$
$$R_e = $$
$$N_u = 0.023 (R_e)^{0.8}(P_r)^n$$
$$n = 0.4\space for\space heating\space of\space fluid$$
$$n = 0.3\space for\space cooling\space of\space fluid$$
$$P_r=0.699$$
$$Nu = $$
$$h = \frac{N_u.k}{D_s}W/m^2K$$
$$k = 0.02756$$
$$h = $$
$$W/m^2K$$
$$Q_c = \frac{h.A}{(T_s - T_a)}W$$
$$A = \pi.D_s.L$$
$$Qc = $$
$$W$$
Copyright © SOLVE The Virtual Lab @ NITK Surathkal




