Consider the following simple C program: Sum of first n natural numbers

#include <stdio.h>

int
main(int argc, char **argv)
{
   int i;
   int sum;
   int n = 10;

  sum = 0;
  for (i = 1; i <= n; i++)
      sum += i;

  printf(Sum of first %d natural numbers is: %d\n", n, sum);
  return 0;

}

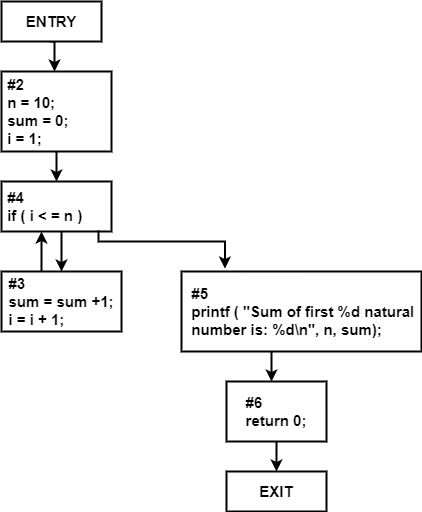
Any sequence of instructions in a program could be represented in terms of basic blocks, and a CFG could be drawn using those basic blocks. For the given C program:

• Identify the basic blocks and verify whether your representation matches with the output produced after compiling your program
• Draw a Control Flow Graph (CFG) using these basic blocks. Again, verify how the CFG generated after compilation relates to the basic blocks identified by the compiler
• Calculate McCabe's complexity from the CFG so obtained

Learning Objectives:

• Identify the basic basic blocks for a given program
• Draw a CFG using the basic blocks
• Determination of McCabe's complexity from a CFG. (McCabe's Cyclomatic complexity can be obtained by: E - N + 2)

Limitations: The current workspace can generate CFGs only for the main function for the above code. In other words, this would not work with user-defined functions. However, in real life a program would contain several modules. All such modules have to be taken into account while determining the complexity.

Consider the following simple C program: Initialize elements of a 2D array to 0

#include <stdio.h>

int
main(int argc, char **argv)
{
   int a[5][10];
   int i;
   int j;
   int nr;
   int nc;

   nr = 5;
   nr = 5;
   nc = 10;

   for (i = 0; i <= nr; i++) {
     for (j = 0; j <= nc; j++) {
       a[i][j] = 0;
     }
   }

   return 0;
}

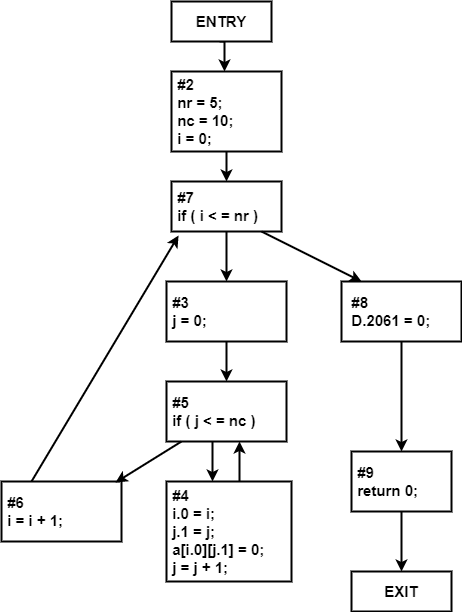
Tasks:

• Compile the above program to generate it's CFG. Verify whetther the CFG corresponds to the basic blocks
• Identify the linearly independent paths from the CFG. The paths would be indicated by the basic block numbers (instead of line numbers of the actual program)

Learning Objectives:

• Identify the basic basic blocks for a given program
• Draw a CFG using the basic blocks
• Determination of McCabe's complexity from a CFG (McCabe's Cyclomatic complexity can be obtained by: E - N + 2)
• Identify the linearly independent paths from a CFG

Limitations: The current workspace can generate CFGs only for the main function for the above code. In other words, this would not work with user-defined functions. However, in real life a program would contain several modules. All such modules have to be taken into account while determining the complexity.

The following C program implements the binary search technique performed over an array of integers. This is an example of a non-trivial program that we often encounter in our lives.

#include <stdio.h>

int
main(int argc, char **argv)
{
   int a[] = {2, 4, 6, 8, 10, 12, 14, 16};
   int key = atoi(argv[1]);
   int n=8;
   int low = 0;
   int high = n - 1;
   int middle;
   int flag = 0

   while (low <= high) {
     middle = (low + high) / 2;
      if (key == a[middle]) {
            printf("Found key %d at position %d\n", key, middle);
            flag = 1;
     }
     else if (key > a[middle]) {
          high = middle - 1;
     }
     else {
          low = middle + 1;
     }
     if (flag)
          break;
   }

     if (! flag)
          printf("Key %d was not found!\n", key);
   return 0;
}

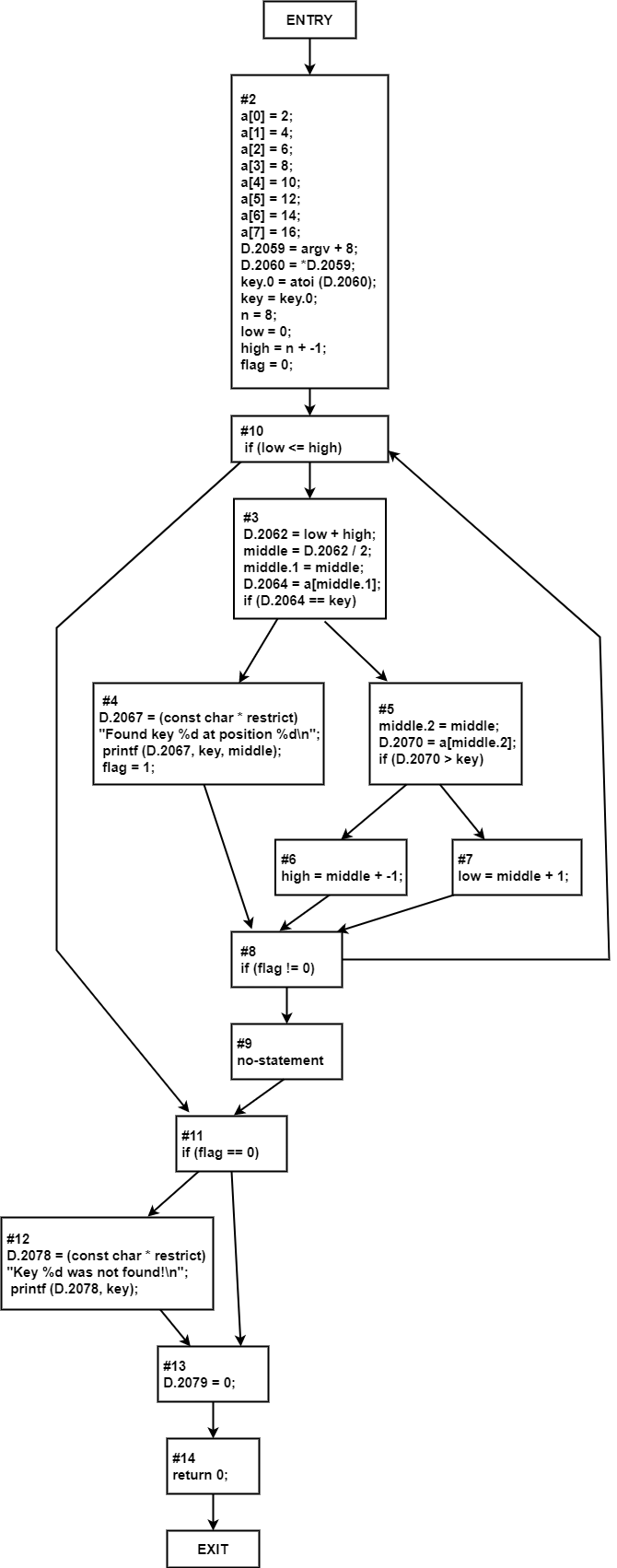
Learning Objectives:

• Determine the cyclomatic complexity of this program (McCabe's Cyclomatic complexity can be obtained by: E - N + 2).
• How would you classify this program in terms of its complexity (simple, complex, unstable)?

Limitations: The current workspace can generate CFGs only for the main function for the above code. In other words, this would not work with user-defined functions. However, in real life a program would contain several modules. All such modules have to be taken into account while determining the complexity.