DSB-SC Modulation

Theory

Double Sideband Suppressed Carrier (DSB-SC) modulation is a type of amplitude modulation where only the sidebands are transmitted, and the carrier signal is suppressed. This method is more power-efficient compared to standard amplitude modulation (AM), as it eliminates the carrier, which does not carry useful information.

Mathematical Representation

The DSB-SC modulated signal \( s(t) \) can be expressed as:

\( s(t) = A_c m(t) \cos(2\pi f_c t) \)

Where:

• \( A_c \) is the amplitude of the carrier signal.
• \( m(t) \) is the baseband (modulating) signal.
• \( f_c \) is the frequency of the carrier signal.

In DSB-SC modulation, the carrier signal \( \cos(2\pi f_c t) \) is multiplied by the modulating signal \( m(t) \), resulting in the modulated signal \( S(t) \). The key characteristic of DSB-SC is that the carrier \( A_c \cos(2\pi f_c t) \) is not transmitted. Instead, only the sidebands generated by the multiplication of \( m(t) \) and \( \cos(2\pi f_c t) \) are transmitted.

Block Diagram

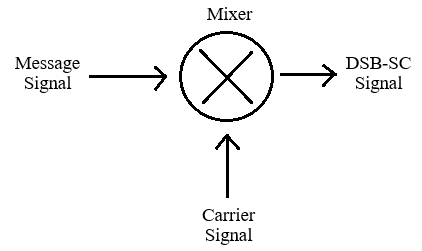
Fig 1: DSB-SC Modulation

Frequency Domain Description

The frequency-domain representation \( S(j\omega) \) of the DSB-SC signal is:

\( S(j\omega) = \frac{1}{2} \left[ M(j(\omega - \omega_c)) + M(j(\omega + \omega_c)) \right] \)

• Where, \( S(j\omega) \) is the fourier transform of the modulated wave s(t).
• Where, \( M(j\omega) \) is the fourier transform of the message signal m(t).
• The message spectrum \( M(j\omega) \) is shifted to center around \( \pm \omega_c \).
• Both upper sideband (USB) and lower sideband (LSB) are present.
• The carrier component is suppressed.

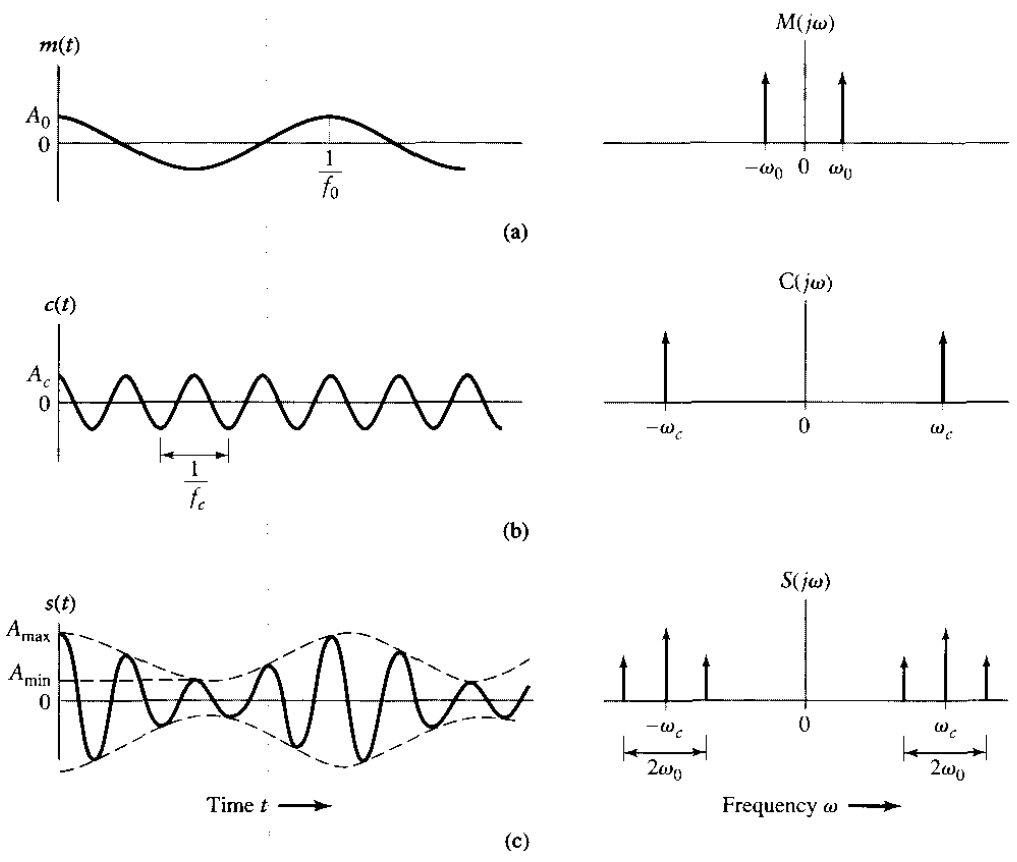
Fig 2: Time-domain (on the left) and frequency-domain (on the right) characteristics of DSB-SC modulation produced by a sinusoidal modulating wave. (a) Modulating wave. (b) Carrier wave. (c) DSB-SC modulated wave.

---

DSB-SC Demodulation

DSBSC Demodulation :

Recovering the message signal from the demodulated signal is performed coherently. That is, the demodulated signal is multiplied by a high-frequency sinusoid in perfect synchronization (in phase and frequency) with the incoming carrier.

This requirement poses a challenge on the design of the demodulator circuit, as it would then require a part for carrier-recovery. Failing to accomplish perfect synchronization will result in phase mismatch or frequency mismatch, leading to some form of distortion in the recovered signal.

Multiplying the modulated signal with a local carrier will produce a baseband signal as well as a signal modulated at double the carrier frequency. Therefore, a LPF is needed at the far end of the demodulator to recover the baseband signal .

Block Diagram

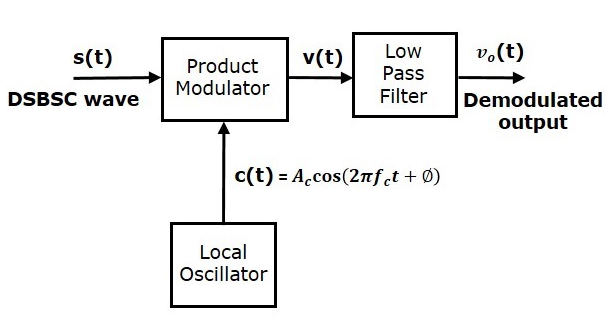
Fig 3: DSB-SC Demodulation