Experiment Setting: The Moving, Shrinking Rectangles
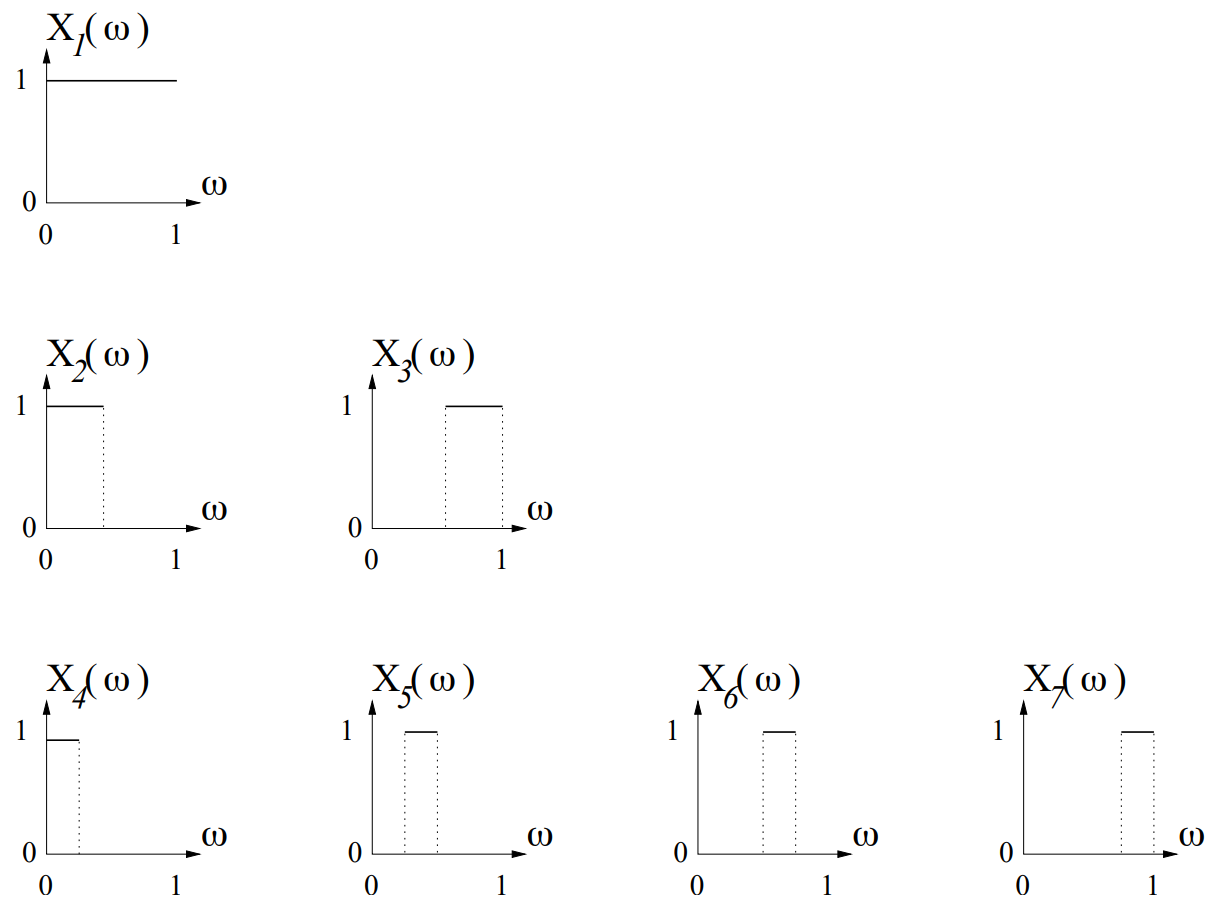
We define a sequence of random variables \(X_n\) on the probability space \(\Omega = (0, 1]\). For each integer \(k \geq 1\), the block of variables from \(X_{2^{k-1}}\) to \(X_{2^k-1}\) are defined. Each variable in this block is 1 on a unique sub-interval of (0, 1] of length \(2^{-(k-1)}\), and 0 otherwise. This sequence converges to 0 in probability because the width of these intervals (i.e., the probability of being 1) shrinks to zero. However, does it converge almost surely?
Observations
Enter values for \(\omega\) and \(k\), then click "Check" to begin the analysis.