Phase Shift Keying (PSK)

Theory:

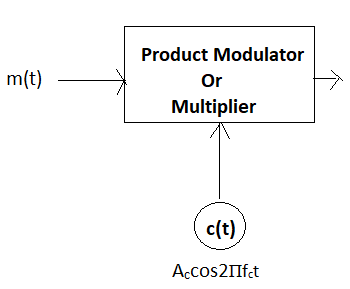
PSK is a digital modulation scheme which is analogues to phase modulation. Binary Phase Shift Keying (BPSK) is the simplest form of PSK. In binary phase shift keying two output phases are possible for a single carrier frequency one out of phase represent logic 1 and logic 0. As the input digital binary signal change state the phase of output carrier shift two angles that are 180o out of phase. In a PSK modulator the carrier input signal is multiplied by the digital data. Each time a change in input logic condition will change the output phase consequently for PSK the output rate of change equal to the input rate range and widest output bandwidth occurs when the input binary data are alternating 1/0 sequence. The fundamental frequency of an alternate 1/0 bit sequence is equal to one half of the bit rate.

PSK Transmitter:

In PSK, binary ‘1’ is represented by the actual carrier, and binary 0 by the 180-degree phase shift of the carrier.

1 => S1(t) = A_ccos2Пf_ct
0 => S2(t) = A_ccos{2Пf_ct + 180⁰} = - A_ccos2Пf_ct

Here, the electric signaling scheme is NRZ
1 = +ve
0 = -ve

PSK Receiver:

For the demodulation of PSK, a soft detector (SD) will be used

1 => A_ccos2Пf_ct.A_ccos2Пf_ct => (Ac)²/2 > V_th
0 => A_ccos2Пf_ct.(-A_ccos2Пf_ct) => -(Ac)²/2 < V_th

a. Constellation Diagram

Energy per bit (Eb):

** for Transmission of binary ‘1’
Eb = ∫₀^Tb(Ac.cos2П.fc.t)² dt
= ∫₀^Tb((Ac)²/2) dt + ∫₀^Tb((Ac)².cos4П.fc.t)/2) dt
= ∫₀^Tb((Ac)²/2) dt + 0 (area = 0 due to complete cycle)
= ((Ac)²/2).Tb
Ac = √(2Eb/Tb)

** for Transmission of binary ‘0’ Eb = ∫₀^Tb(-Ac.cos2П.fc.t)² dt
= ∫₀^Tb((Ac)²/2) dt + ∫₀^Tb((Ac)².cos4П.fc.t)/2) dt
= ∫₀^Tb((Ac)²/2) dt + 0 (area = 0 due to complete cycle)
= ((Ac)²/2).Tb
Ac = √(2Eb/Tb)

** Constellation Diagram
1 => S1(t) = Ac.cos2П.fc.t = √(2Eb/Tb).cos2Пf_ct = √(Eb). √(2/Tb).cos2Пf_ct
0 => S2(t) = -Ac.cos2П.fc.t = -√(2Eb/Tb).cos2Пf_ct = -√(Eb). √(2/Tb).cos2Пf_ct

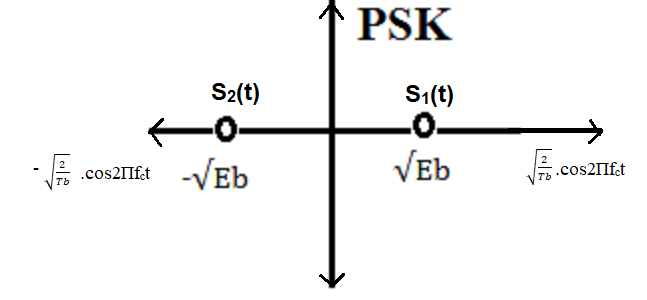
Figure: Constellation Diagrams of PSK

So, energy of S1(t) = (√(Eb))² = Eb
So, energy of S2(t) = (-√(Eb))² = Eb

Distance between the signaling points, d12 = 2(√(Eb))

High-order PSK (e.g., 8 PSK, 16 PSK) can transmit more bits per symbol but is more sensitive to noise. Low-order PSK (e.g., BPSK, QPSK) is less susceptible to noise.
PSK modulation can be visualized using a constellation diagram, where each point represents a symbol. In the presence of noise, points may be away from the original positions, making them harder to distinguish.

b. Under different noise configurations

PSK Modulation with AWGN
In PSK modulation, digital data is represented by varying the phase of the carrier signal. Binary PSK (BPSK) is a common form of PSK modulation where the carrier phase is shifted by 180 degrees for different binary symbols.

Mathematically, the PSK-modulated signal x(t) can be represented as:
x(t) = A_ccos2Пf_ct, { for binary symbol 1}
x(t) = A_ccos(2Пf_ct + 180), { for binary symbol 0}

Where:
fc is the carrier frequency.
Ac is the carrier amplitude.

In the presence of AWGN, the received signal y(t) becomes:
y(t) = x(t) + n(t)
Where:
x(t) is the PSK-modulated signal.
n(t) is the AWGN.

The AWGN introduces noise across all phases and amplitudes, impacting the phase shifts of the PSK signal. Since PSK relies on phase differences for symbol differentiation, the noise can cause phase shifts, leading to errors in demodulation. The SNR (signal-to-noise ratio) plays a crucial role in determining the quality of demodulation.

PSK Modulation with Rayleigh Fading:
Rayleigh fading introduces random amplitude and phase variations to the received signal due to multipath propagation. In the case of PSK modulation, the mathematical representation of the received signal (y(t) under Rayleigh fading is:
y(t) = h . x(t) + n(t)
Where:
h is the complex fading coefficient.
x(t) is the PSK-modulated signal.
n(t) is the noise.

The fading coefficient h introduces random variations in both amplitude and phase to the signal components. These variations affect the phases of the PSK signal, potentially leading to errors in phase detection and symbol demodulation.

PSK modulation under different noise configurations involves adding noise to the modulated signal. AWGN introduces phase and amplitude noise across all phases, affecting PSK symbol differentiation. Rayleigh fading introduces random amplitude and phase variations due to multipath propagation, impacting the phase of the PSK signal. The reliability of PSK demodulation depends on the SNR for AWGN and the characteristics of the fading channel for Rayleigh fading.

c. Under Different Scenarios

Phase Shift Keying (PSK) is a modulation technique where the phase of a carrier signal is varied to transmit digital information. The performance of PSK modulation can vary in different scenarios based on factors such as signal-to-noise ratio (SNR), noise, interference, and channel conditions.

High SNR (Low Noise):
PSK modulation performs well in scenarios with high SNR and low noise levels. The different phase shifts corresponding to binary states can be accurately detected at the receiver, leading to accurate data detection and low error rates.

Low SNR (High Noise):
PSK modulation is sensitive to phase changes, which can lead to errors in low SNR scenarios due to noise-induced phase fluctuations. In situations with low SNR and high noise, the receiver might struggle to distinguish the correct phase shifts, leading to increased error rates.

Modulation Index:
The choice of modulation index, which defines the phase separation between different symbols, can impact PSK modulation's performance. In some scenarios, a larger modulation index can lead to better differentiation between phases, while in others, it might increase susceptibility to phase noise.

Interference and Crosstalk:
PSK modulation can be affected by interference and crosstalk, which can lead to phase shifts in the received signal. Interference can cause phase ambiguity, resulting in errors in phase detection at the receiver.

Frequency Selective Fading:
Similar to other modulation techniques, PSK modulation can experience frequency-selective fading, which can distort the phase of the received signal. Rapid phase changes due to fading can lead to difficulties in accurate phase detection.

Channel Distortion:
Distortions introduced by the communication channel, such as phase shifts or amplitude changes, can affect the received PSK signal. These distortions can lead to errors in phase detection and, consequently, data detection.

Coherent Detection:
Coherent detection of PSK modulation requires carrier synchronization at the receiver. In scenarios where carrier synchronization is challenging, phase errors can accumulate over time, degrading the overall system performance.

Adaptive Modulation:
Adaptive modulation techniques can be employed with PSK to dynamically adjust the modulation index or constellation size based on channel conditions. This allows for optimization of data rate and reliability according to the scenario.

Error Correction Coding:
Like other modulation techniques, adding error correction codes can enhance PSK modulation's performance in noisy environments. These codes provide redundancy, allowing the receiver to correct errors caused by noise or phase fluctuations.
PSK modulation offers advantages in scenarios with favorable SNR and can be sensitive to phase changes in noisy or interference-prone environments. Its performance depends on factors like modulation index, carrier synchronization, and the presence of noise or distortion. Employing techniques such as error correction coding and adaptive modulation can help optimize PSK modulation's performance in various scenarios.