Amplitude Shift Keying (ASK)

Theory:

Amplitude shift keying (ASK) is the simplest digital modulation technique. In this modulation method there is only one carrier which is switched ON/OFF depending upon the input binary sequence to transmit symbol 0 and 1. The binary ASK system was one of the earliest form of digital modulation used in wireless telegraphy. In an binary ASK system binary symbol 1 is represented by transmitting a sinusoidal carrier wave of fixed amplitude Ac and fixed frequency fc for the bit duration Tb where as binary symbol 0 is represented by switching of the carrier for Tb seconds. This signal can be generated simply by turning the carrier of a sinusoidal oscillator ON and OFF for the prescribed periods indicated by the modulating pulse train. For this reason the scheme is also known as on-off shift testing. The ASK signal can be generated by applying the incoming binary data and the sinusoidal carrier to the two inputs of a product modulator. The resulting output is the ASK wave.

In this modulation, binary 1 is represented by the presence of a carrier and binary 0 by the absence of a carrier.

ASK Transmitter:

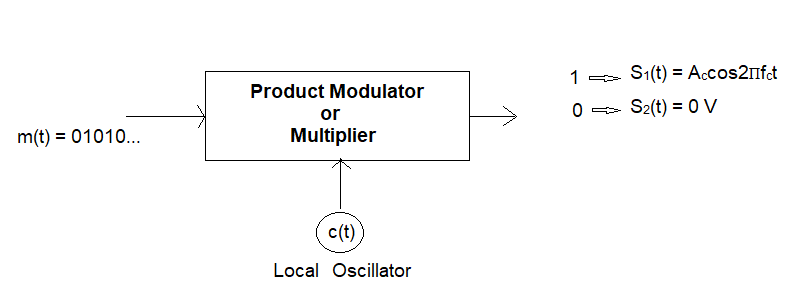
Here, the electrical signal representation technique is ON-OFF coding. In which
1 => +ve
0 => 0 V

ASK Receiver:

For the demodulation of ASK, a soft detector (SD) will be used
1 => Ac² cos²2Пf_ct 1 => (Ac)²/2
0 => 0 0 => 0 V

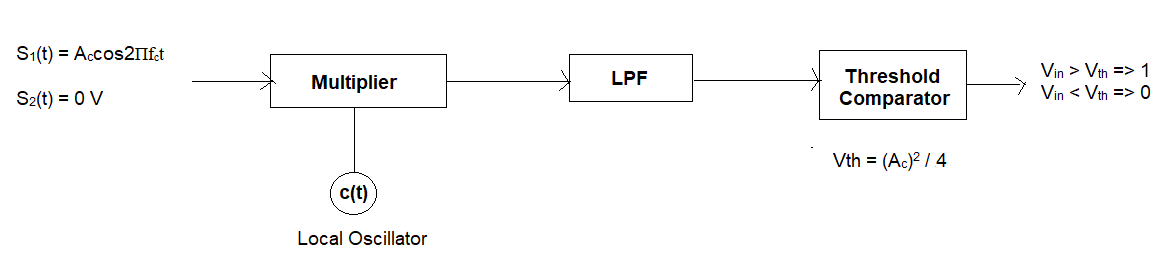
Since the soft detector is used, we have to observe whether either one occurs or not.

a. Constellation Diagram

Energy per bit (Eb):

We know that all periodic signals are power signals. Now we’ll find the energy of ASK for the transmission of binary ‘1’.

Eb = ∫₀^Tb(Ac.cos2П.fc.t)² dt
= ∫₀^Tb(Ac)².(cos2П.fc.t)² dt
=∫₀^Tb((Ac)²/2) dt + ∫₀^Tb((Ac)².cos4П.fc.t)/2) dt
= ∫₀^Tb((Ac)²/2) dt + 0 (area = 0 due to complete cycle)
**where Ac is the amplitude of the carrier signal fc is the carrier frequency in Hz

To save transmitter energy, Eb should be small.
Eb = ((Ac)²/2).Tb (where Tb is the bit duration)

** for transmission of binary ‘0’
Eb = ∫₀^Tb(S₂(t))²dt = 0

** Constellation Diagram
1 => S₁(t) = Ac.cos2П.fc.t = √(2Eb/Tb).cos2Пf_ct
0 => S₂(t) = 0

Eb = ∫₀^Tb(S₁(t))²dt
= ∫₀^Tb(√(2Eb/Tb).cos2Пfct)² dt
= Eb . ∫₀^Tb(√(2/Tb).cos2Пf_ct)² dt
= ∫₀^Tb(√(2/Tb).cos2Пf_ct)² dt = 1

** In constellation diagram the function whose energy is equal to 1 is said to be a normalized function.
Now, S₁(t) = Eb . √(2/Tb).cos2Пf_ct & S₂(t) = 0

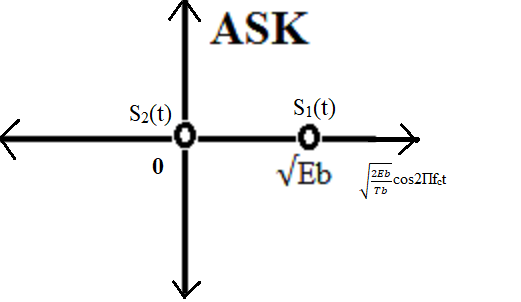
Figure: Constellation Diagram of Binary ASK

In the above figure the reference axes corresponds to normalized functions.

Distance of S1(t) from origin is √(Eb). Energy of S1(t) = {√(Eb)}² = Eb.
Distance of S2(t) from origin is 0. Energy of S2(t) = 0
Distance between signaling points, d12 = √(Eb)
High-order Amplitude Shift Keying (ASK) refers to using a large number of amplitude levels to represent digital data. For instance, in binary ASK (BASK), there are two amplitude levels, usually represented as 0 and 1. High-order ASK can have more than two amplitude levels, such as 4, 8, 16, 64, etc.

b. Under different noise configurations

Let's explore ASK modulation under two common noise scenarios: AWGN (Additive White Gaussian Noise) and Rayleigh fading.

ASK Modulation with AWGN:

We've already discussed the effect of AWGN on ASK modulation in the previous response. The mathematical effect involves adding Gaussian-distributed noise to the modulated signal. The received signal y(t) is given by:
y(t) = x(t) + n(t)
Where:
x(t) is the modulated ASK signal.
n(t) is the AWGN.
The effect of AWGN is to add random variations to the amplitude of the signal, which can lead to erroneous detection of the transmitted symbols. The SNR (signal-to-noise ratio) plays a crucial role in determining the quality of demodulation, with higher SNR values leading to better performance.

ASK Modulation with Rayleigh Fading:

Rayleigh fading is a type of multipath fading that occurs in wireless communication channels. It's characterized by a random variation in the amplitude of the received signal due to constructive and destructive interference of multiple signal paths.

Mathematically, Rayleigh fading can be represented as a complex Gaussian random variable with zero mean and a certain variance. The received signal y(t) in the presence of Rayleigh fading can be represented as:
y(t) = h . x(t) + n(t)
Where:
h is the complex fading coefficient, representing the channel gain and phase shift.
x(t) is the modulated ASK signal.
n(t) is the noise

The fading coefficient h introduces random amplitude and phase variations to the signal. Due to the randomness of h, the received signal's amplitude will experience fluctuations, impacting the detection of transmitted symbols. The actual fading distribution might vary depending on the specific channel characteristics.

When ASK modulation is subjected to different noise configurations, the mathematical representation of the received signal changes. Under AWGN, Gaussian noise is added to the signal's amplitude. Under Rayleigh fading, the complex fading coefficient introduces random amplitude and phase variations. The performance of ASK modulation in these scenarios depends on the SNR for AWGN and the characteristics of the fading channel for Rayleigh fading.

c. Under Different Scenarios

Amplitude Shift Keying (ASK) is a modulation technique that varies the amplitude of a carrier signal to convey digital information. The behavior of ASK modulation can vary in different scenarios based on factors like noise, signal-to-noise ratio (SNR), and channel characteristics.

Low Noise Environment:
In a scenario with low noise and a high SNR, ASK modulation tends to perform well. The transmitted signal's amplitude variations are accurately detected at the receiver, resulting in reliable data transmission. The demodulator can easily distinguish between the different amplitude levels, leading to low error rates.

High Noise Environment:
In the presence of high noise levels, ASK modulation can become less reliable. The noise can lead to amplitude fluctuations in the received signal, making it challenging for the receiver to accurately detect the intended amplitude levels. This can result in higher bit error rates and decreased communication reliability compared to scenarios with lower noise levels.

Multi-Path Fading Channels:
In scenarios with multi-path fading channels, where the transmitted signal takes multiple paths due to reflections and scattering, ASK modulation might experience fading. Fading can lead to rapid changes in signal amplitude at the receiver, causing difficulties in demodulation. To combat fading, techniques like diversity reception and error correction coding can be employed.

Frequency Selective Channels:
ASK modulation can be affected by frequency-selective channels, where certain frequency components of the signal experience more attenuation than others. This can result in distortion of the amplitude-modulated signal, leading to errors in detection at the receiver.

Varying Signal Amplitude:
ASK modulation relies on varying the carrier signal's amplitude. If the transmitted signal encounters amplifiers or attenuators along its path, the modulation depth can change, affecting the ability to accurately detect the signal's amplitude variations at the receiver.

Adaptive Modulation:
In some scenarios, adaptive modulation techniques can be used with ASK. This involves dynamically changing the modulation depth or constellation points based on the changing channel conditions. In good channel conditions, higher modulation levels (larger constellation points) can be used for increased data rates, while in poor conditions, lower modulation levels can be employed for better reliability.

Error Correction Coding:
To improve ASK modulation's performance in noisy environments, error correction codes can be employed. These codes add redundancy to the transmitted data, allowing the receiver to correct errors that might have occurred during transmission. This is particularly useful in scenarios where ASK modulation alone might result in unacceptably high error rates.

In summary, ASK modulation's performance is influenced by noise, channel characteristics, and modulation depth. While ASK is straightforward to implement, it might not be as robust as other modulation techniques like Phase Shift Keying (PSK) or Quadrature Amplitude Modulation (QAM) in scenarios with significant noise or fading. Therefore, the choice of modulation technique should be based on the specific requirements and challenges of the communication scenario.