Phase Shift Keying (PSK)

Theory:

PSK is a digital modulation scheme which is analogous to phase modulation. Binary Phase Shift Keying (BPSK) is the simplest form of PSK. In Binary Phase Shift Keying, two output phases are possible for a single carrier frequency, where one phase represents logic 1 and the other represents logic 0. As the input digital binary signal changes state, the phase of the output carrier shifts by 180 degrees. In a PSK modulator, the carrier input signal is multiplied by the digital data. Each change in the input logic condition will change the output phase. Consequently, for PSK, the output rate of change equals the input rate range, and the widest output bandwidth occurs when the input binary data are an alternating 1/0 sequence. The fundamental frequency of an alternating 1/0 bit sequence is equal to one half of the bit rate.

PSK Transmitter:

In PSK, binary ‘1’ is represented by the actual carrier, and binary ‘0’ by the 180-degree phase shift of the carrier.

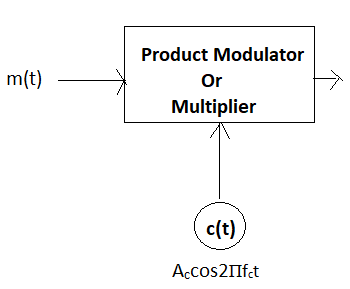
For binary '1': $S_1(t) = A_c \cos(2\Pi f_c t)$
For binary '0': $S_2(t) = A_c \cos(2\Pi f_c t + 180^\circ) = -A_c \cos(2\Pi f_c t)$

Here, the electric signaling scheme is Non-Return-to-Zero (NRZ):
1 = +ve voltage
0 = -ve voltage

PSK Receiver:

For the demodulation of PSK, a soft detector (SD) will be used.

If the received signal is $A_c \cos(2\Pi f_c t)$, then after multiplication and integration:
Output for '1': $A_c \cos(2\Pi f_c t) \cdot A_c \cos(2\Pi f_c t) \implies (A_c)^2/2 > V_{th}$
Output for '0': $A_c \cos(2\Pi f_c t) \cdot (-A_c \cos(2\Pi f_c t)) \implies -(A_c)^2/2 < V_{th}$
where $V_{th}$ is the threshold voltage.

Constellation Diagram of PSK

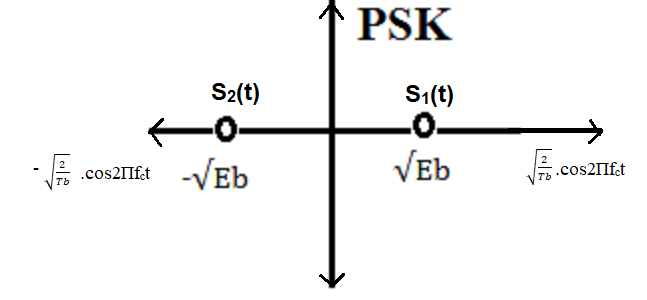
Figure: Constellation Diagram of BPSK

So, energy of $S_1(t) = (\sqrt{E_b})^2 = E_b$
So, energy of $S_2(t) = (-\sqrt{E_b})^2 = E_b$

Distance between the signaling points, $d_{12} = 2(\sqrt{E_b})$

High-order PSK (e.g., 8-PSK, 16-PSK) can transmit more bits per symbol but is more sensitive to noise. Low-order PSK (e.g., BPSK, QPSK) is less susceptible to noise.
PSK modulation can be visualized using a constellation diagram, where each point represents a symbol. In the presence of noise, points may be displaced from their original positions, making them harder to distinguish.

Under Different Noise Configurations

PSK Modulation with Additive White Gaussian Noise (AWGN)
In PSK modulation, digital data is represented by varying the phase of the carrier signal. Binary PSK (BPSK) is a common form of PSK modulation where the carrier phase is shifted by 180 degrees for different binary symbols.

Mathematically, the PSK-modulated signal $x(t)$ can be represented as:
$x(t) = A_c \cos(2\Pi f_c t)$, { for binary symbol 1}
$x(t) = A_c \cos(2\Pi f_c t + 180^\circ)$, { for binary symbol 0}

Where:
$f_c$ is the carrier frequency.
$A_c$ is the carrier amplitude.

In the presence of AWGN, the received signal $y(t)$ becomes:
$y(t) = x(t) + n(t)$
Where:
$x(t)$ is the PSK-modulated signal.
$n(t)$ is the AWGN.

The AWGN introduces noise across all phases and amplitudes, impacting the phase shifts of the PSK signal. Since PSK relies on phase differences for symbol differentiation, the noise can cause phase shifts, leading to errors in demodulation. The SNR (signal-to-noise ratio) plays a crucial role in determining the quality of demodulation.

PSK Modulation with Rayleigh Fading:
Rayleigh fading introduces random amplitude and phase variations to the received signal due to multipath propagation. In the case of PSK modulation, the mathematical representation of the received signal $y(t)$ under Rayleigh fading is:
$y(t) = h \cdot x(t) + n(t)$
Where:
$h$ is the complex fading coefficient.
$x(t)$ is the PSK-modulated signal.
$n(t)$ is the noise.

The fading coefficient $h$ introduces random variations in both amplitude and phase to the signal components. These variations affect the phases of the PSK signal, potentially leading to errors in phase detection and symbol demodulation.

PSK modulation under different noise configurations involves adding noise to the modulated signal. AWGN introduces phase and amplitude noise across all phases, affecting PSK symbol differentiation. Rayleigh fading introduces random amplitude and phase variations due to multipath propagation, impacting the phase of the PSK signal. The reliability of PSK demodulation depends on the SNR for AWGN and the characteristics of the fading channel for Rayleigh fading.