Frequency Shift Keying (FSK)

Theory:

Frequency-Shift Keying (FSK) is a frequency modulation scheme in which digital information is transmitted through discrete frequency changes of a carrier wave. The simplest form of FSK is Binary FSK (BFSK), which uses a pair of discrete frequencies to transmit binary (0s and 1s) information. With this scheme, the frequency representing a "1" is called the mark frequency (f₁) and the frequency representing a "0" is called the space frequency (f₂). If the incoming bit is 1, a signal with frequency f₁ is sent for the duration of the bit. If the bit is 0, a signal with frequency f₂ is sent for the duration of this bit. This is the basic principle behind FSK modulation.

FSK Transmitter:

In this binary scheme, '1' is represented by a higher frequency carrier (say, f₁) and binary '0' by a lower frequency carrier (say, f₂).

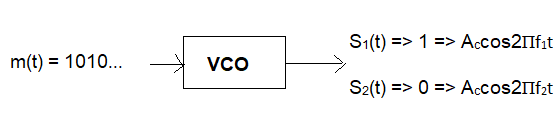
VCO (Voltage Controlled Oscillator):

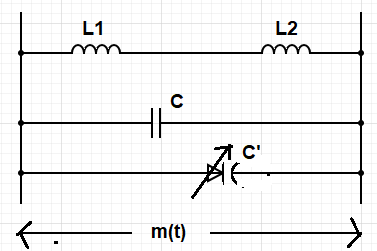
The output frequency (f_i) of the LC tank circuit in the VCO is given by:
f_i = 1 / (2П√((L₁+L₂)(C+C')) )

FSK Receiver:

The figure below illustrates a coherent FSK receiver. This type of receiver uses two correlators, each matched to one of the possible FSK frequencies (f₁ for binary '1' and f₂ for binary '0').

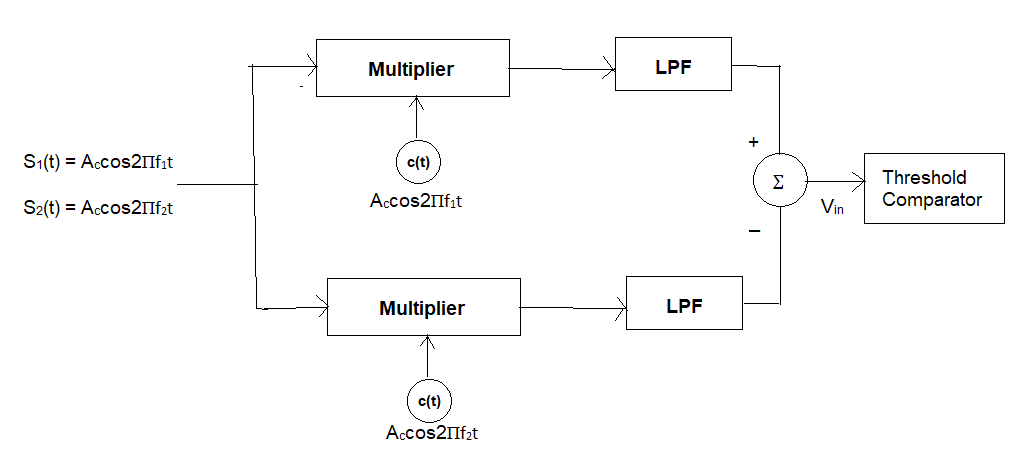
The received FSK signal, r(t), is fed into both branches of the receiver. Each branch mixes r(t) with its respective local carrier (e.g., cos(2Пf₁t) or cos(2Пf₂t)) and then integrates the product over the bit duration T_b.

Let's denote the output of the upper correlator (matched to f₁) as Y₁ and the output of the lower correlator (matched to f₂) as Y₂.

• If binary '1' (A_ccos(2Пf₁t)) was transmitted:
  • Y₁ will have a significant positive value (proportional to E_b).
  • Y₂ will be close to zero, assuming f₁ and f₂ are orthogonal over T_b.
• If binary '0' (A_ccos(2Пf₂t)) was transmitted:
  • Y₁ will be close to zero.
  • Y₂ will have a significant positive value (proportional to E_b).

The difference between these two correlator outputs, Y₁ - Y₂, is then fed to a threshold comparator.

• If Y₁ - Y₂ > 0 (or a threshold close to 0), the receiver decides '1'.
• If Y₁ - Y₂ < 0 (or a threshold close to 0), the receiver decides '0'.

In an ideal scenario with no noise and perfectly orthogonal frequencies:
- If '1' is sent, Y₁ ≈ E_b and Y₂ ≈ 0, so the difference is E_b.
- If '0' is sent, Y₁ ≈ 0 and Y₂ ≈ E_b, so the difference is -E_b.
The optimal decision threshold for binary FSK in AWGN is typically 0 V.

Constellation Diagram of FSK

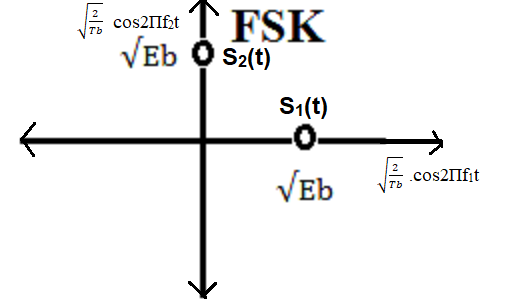
Figure: Constellation diagram of FSK

In the above figure, the points are plotted in terms of the coordinates along the two orthogonal basis functions.
The distance between signaling points, d₁₂ = √( (√(E_b) - 0)² + (0 - √(E_b))² ) = √(E_b + E_b) = √(2E_b).
Due to the orthogonality of the basis functions, the signal points in the constellation diagram lie on perpendicular axes, forming a 90-degree angle between their vector representations.

High-order frequency shift keying (FSK) refers to using a larger number of frequency shifts to represent multiple symbols or bits of digital data. In FSK, each frequency represents a unique symbol or set of bits. High-order FSK schemes enable higher data rates but can also be more susceptible to noise and channel impairments.

Under different noise configurations

FSK Modulation with AWGN:
In FSK modulation, digital data is represented by varying the frequency of the carrier signal. Let's consider a basic case of binary FSK with two different carrier frequencies f₁ and f₂, corresponding to the two binary symbols.

Mathematically, the FSK-modulated signal x(t) can be represented as:
x(t) = A_ccos(2Пf₁t), { for binary symbol 1}
x(t) = A_ccos(2Пf₂t), { for binary symbol 0}

In the presence of AWGN, the received signal y(t) becomes:
y(t) = x(t) + n(t)
Where:
x(t) is the FSK-modulated signal.
n(t) is the AWGN.

The AWGN introduces noise across all frequencies, affecting both the amplitudes and phases of the signal components. Since FSK relies on frequency differences for symbol differentiation, the noise can cause frequency shifts and amplitude variations, leading to errors in demodulation. The impact of noise can be quantified using the SNR (signal-to-noise ratio).

FSK Modulation with Rayleigh Fading:
Rayleigh fading, as discussed previously, introduces random amplitude and phase variations to the received signal due to multipath propagation. In the case of FSK modulation, the mathematical representation of the received signal y(t) under Rayleigh fading is:

y(t) = h . x(t) + n(t)
Where:
h is the complex fading coefficient.
x(t) is the FSK-modulated signal.
n(t) is the noise.

The fading coefficient h introduces random variations in both amplitude and phase to the signal components. As a result, the amplitudes and phases of the two carrier frequencies can experience fluctuations due to fading, potentially causing errors in symbol detection.

FSK modulation under different noise configurations involves adding noise to the modulated signal. AWGN introduces amplitude and phase noise across all frequencies, affecting the differentiation between FSK symbols. Rayleigh fading introduces random amplitude and phase variations due to multipath propagation, impacting the signal's components. In both cases, the reliability of FSK demodulation depends on the SNR for AWGN and the characteristics of the fading channel for Rayleigh fading.