Amplitude Shift Keying (ASK)

Theory:

Amplitude Shift Keying (ASK) is one of the simplest digital modulation techniques. In this method, a carrier signal is switched ON or OFF to represent binary data. In a binary ASK (BASK) system, binary symbol '1' is represented by transmitting a sinusoidal carrier of amplitude A_c and frequency f_c for a duration T_b (bit duration). Binary symbol '0' is represented by the absence of the carrier during the same duration.

This scheme is also called On-Off Keying (OOK). It can be implemented by controlling a carrier oscillator using the binary input signal. When the input is '1', the carrier is transmitted; when the input is '0', the carrier is not transmitted.

ASK Transmitter:

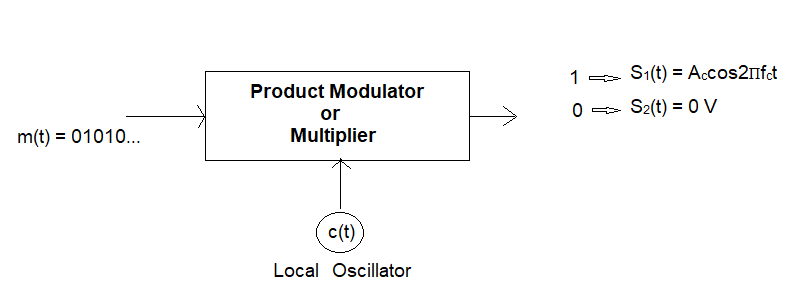
Fig 1: BASK (OOK) Transmitter

ASK Receiver:

At the receiver, the objective is to determine whether the carrier is present or absent during each bit interval. A coherent detector (correlator or matched filter) is commonly used.

• For binary '1' (carrier present): the detector output is proportional to the received signal energy, approximately A_c² T_b / 2.
• For binary '0' (carrier absent): the detector output is close to zero.

A threshold detector compares this output with a predefined value to decide whether a '1' or '0' was transmitted.

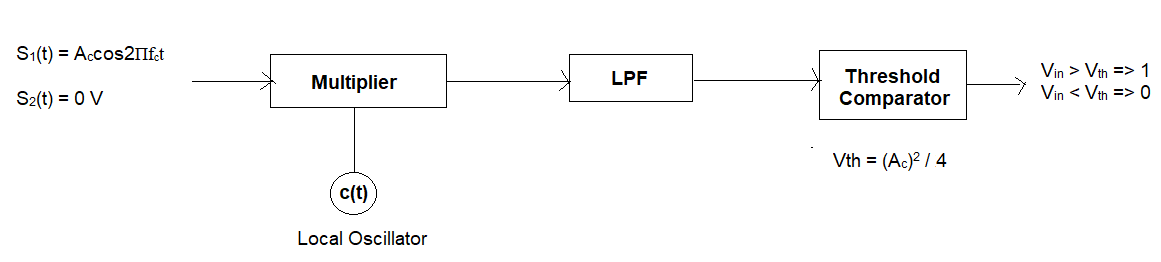
Fig 2: Coherent BASK Receiver

Constellation Diagram of ASK

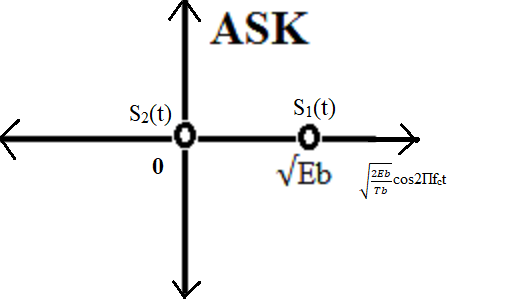
Fig 3: Constellation Diagram of BASK

The ASK signal is represented in a one-dimensional signal space using a single orthonormal basis function.

A single orthonormal basis function is a waveform with unit energy, i.e., \[ \int_0^{T_b} \phi_1^2(t)\, dt = 1 \] Only one basis function is required because ASK varies only in amplitude (one dimension).

The carrier signal \( \cos(2\pi f_c t) \) has energy \( \frac{T_b}{2} \) over the interval \( 0 \le t \le T_b \), so it is scaled to obtain a unit-energy basis function: \[ \phi_1(t) = \sqrt{\frac{2}{T_b}} \cos(2\pi f_c t), \quad 0 \le t \le T_b \]

Any transmitted signal can then be written as: \[ s(t) = a \, \phi_1(t) \] where a is a scalar coefficient representing the signal in signal space.

Using this basis function, the transmitted signals are:

• For binary '1': \[ s_1(t) = \sqrt{E_b} \, \phi_1(t) \] This corresponds to a point at distance \( \sqrt{E_b} \) from the origin.
• For binary '0': \[ s_2(t) = 0 \] This corresponds to the origin.

Therefore:

• Energy of symbol '1' = \(E_b\)
• Energy of symbol '0' = 0
• Distance between the two signal points: \[ d_{12} = \sqrt{E_b} \]

The constellation lies along a single axis (in-phase axis), since ASK uses only amplitude variation and no phase component.

Effect of Noise

ASK with AWGN:

In the presence of Additive White Gaussian Noise (AWGN), the received signal is:
\( y(t) = x(t) + n(t) \)
where:
x(t) = transmitted ASK signal
n(t) = noise

The noise introduces random variations in amplitude, which may cause incorrect detection of symbols. Performance depends on the signal-to-noise ratio (SNR).

ASK with Rayleigh Fading:

In wireless channels, multipath propagation can cause fading. The received signal is modeled as:
\( y(t) = h \cdot x(t) + n(t) \)
where:
h = channel coefficient (random amplitude and phase)
x(t) = transmitted signal
n(t) = noise

The factor h causes fluctuations in the signal amplitude, making detection more difficult. System performance depends on both SNR and channel conditions.