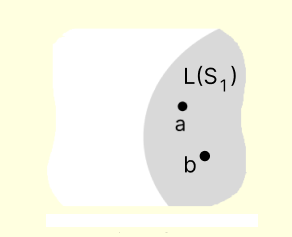
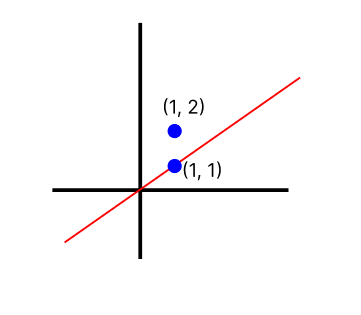
CASE 3 : (i) S = {a}, a ≠ 0

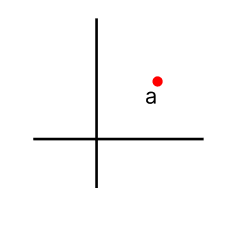
What do you infer?

/

α . a = 0 ⇒ α = 0, α ∈ F

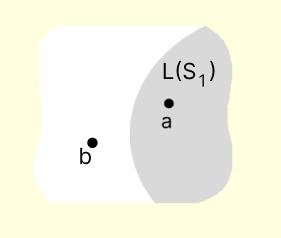
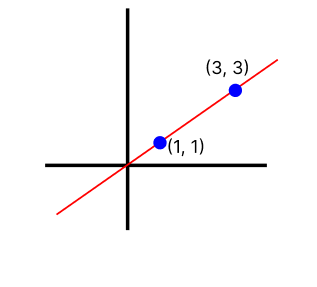
(ii) S = {a}, a = 0

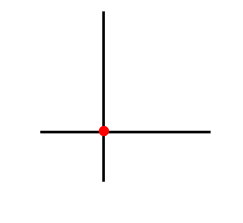
What do you infer?

/

α . 0 = 0, α ≠ 0, α ∈ F

CASE 4 : S ≠ {.} , ϕ and 0 ∉ S   

To understand this case, let S = {a, b} & S₁ = {a}

i) b ∈ L(S₁)

What do you infer?

/

ii) b ∉ L(S₁)

What do you infer?

/

Example 1a: S = {(1, 1), (1, 2)}

S is LINEARLY INDEPENDENT

Click here for reason

b ≡ (1, 2) ∉ L({(1, 1)})

α . (1, 1) + β . (1, 2) = (0, 0)
  ⇒ (α + β , α + 2β) = (0, 0)
  ⇒ α + β = 0 , α + 2β = 0
  ⇒ α = 0 , β = 0

Example 1b: S = {(1, 1), (3, 3)}

S is LINEARLY DEPENDENT

Click here for reason

b ≡ (3, 3) ∈ L({(1, 1)}) ⇒

(3, 3) = 3(1, 1)
3(1, 1) + (-1) (3, 3) = (0, 0)

Example 2:

S = {(), ()}

Submit